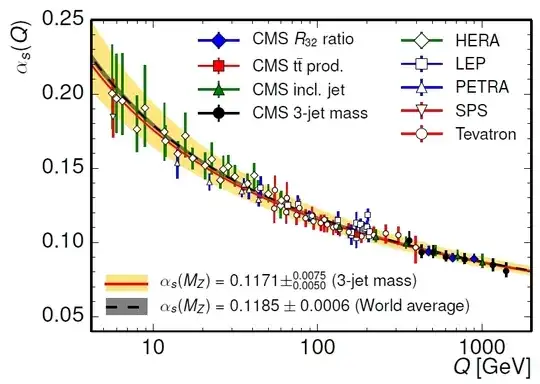
It is well known that couplings change depending on the scale $Q$ at they are measured. This effect is experimentally well documented:
From a theoretical point of view, the running $\alpha_S(\mu)$ can be calculated using the renormalized group equations. However, it is regularly argued that the parameter $\mu$ appears here is a "fake parameter", has no meaning and can always be chosen at will. In particular, it is argued that we can use the fact that "physical observables must be independent of the fake parameter $\mu$ to figure out how the lagrangian parameters $m$ and $g$ must change with $\mu$."
The renormalized group equations that we find this way are then regularly used to calculate the running of parameters like $\alpha_S$:
How does this fit together? In particular, what's the exact relationship between the measured energy dependence of parameters and the running of parameters with the fake parameter $\mu$?
Or formulated differently, if the renormalization group equations encode the dependence on the "fake parameter" $\mu$, which equations describe the dependence on the physical energy scale $Q$?
(I'm aware that there are lots of related questions, but none of them seemed to answer this question unambiguously.)