We are sending huge amount of debris into space from earth, and also very heavy satellites and rockets, then the mass of earth must be decreasing over time. If the mass will decrease, then gravitational attraction between earth and sun must decrease, and its angular momentum must decrease, which would result in greater orbit of earth and earth being cooler over the time, but instead the temperature of earth is increasing, why is it so?
7 Answers
The existing answers are already sufficient, but it is also important to emphasise that if a satellite is sent to Earth orbit, then the launch does not affect the Earth's orbit around the Sun, because the Earth and the satellite continue to interact gravitationally, and the angular momentum of the Earth+satellite system is unchanged.
For there to be any effect on Earth's orbit, the spacecraft needs to be sent off into deep space (i.e. so it is no longer gravitationally bound to Earth), and only a select few spacecraft have been sent there.
As mentioned previously, the total mass and momentum of the spacecraft that have made it to space is negligible compared to the inertia of the Earth's mass. Selecting down to the couple dozen spacecraft that have left the system makes that comparison even more lopsided.
- 137,480
The mass of material sent into orbit may seem huge to a naïve observer, but it is nothing at all compared to the mass of the Earth and wouldn't result in any detectable change in its orbit or rotation. Meanwhile, the mass of the Earth is actually increasing as it picks up dust, meteorites and micro-meteorites on its passage around the sun. A certain amount of the upper atmosphere is gradually leaking into space, but that is more than offset by the space debris which arrives. The majority of orbiting satellites will eventually fall back to Earth.
- 1,748
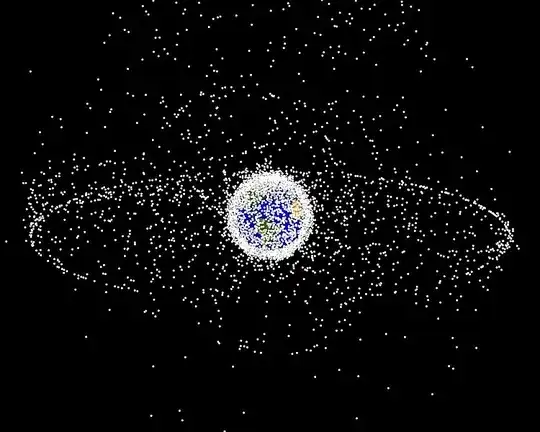
Not only is the mass tiny (as explained in other answers), considerable amount of material is outside the equatorial plane (see image below). Objects orbit in a plane, and the angle this plane makes with the equator is called inclination. The larger the inclination angle, the less of a decrease in Earth's angular momentum will occur.
- Zero degrees of inclination means the object stays in the plane of the equator ("equatorial orbit").
- An inclination between 0° and 90° means the object moves in the same direction as the Earth ("prograde").
- An inclination of 90° means the object moves purely north and south, around the poles ("polar orbit").
- An inclination between 90° and 180° moves in the opposite direction of the Earth ("retrograde") and actually adds to the Earth's angular momentum.
- An inclination of 180° would be a retrograde equatorial orbit.
Are there reasons for using specific orbits?
- The only kind of orbit that stays over one place on the ground is a geostationary orbit. These must be done with a 0° inclination, because any other inclination will make the satellite's latitude move north and south through each orbit. At first, you might think a geostationary orbit would be perfect for taking pictures of things on the Earth. However, the high altitude of geostationary satellites means you are far away from your target, and you are never directly overhead anything other than what is on the equator.
- If you want to take pictures of the entire Earth's surface (spy/mapping/weather satellites), the only orbit that includes the poles is a polar orbit. Inclinations close to 90° are often "good enough", even if they aren't purely polar.
- So your spy satellite takes pictures of a site, but each time the angle of the sun is different and the shadows are all different. What you need is a sun-synchronous orbit. This orbit precesses exactly once each year, which means each time you take a picture, the sun will illuminate the target at the same angle in the sky. The inclination of these orbits tend to be between 90° and 100°, making them slightly retrograde.
- Another use of a sun-synchronous orbit is to have a satellite permanently ride along the Earth's day-night terminator (the sunrise/sunset line). This means that the satellite will never be in shadow behind the Earth. Perfect if you need solar power!
- Satellites that perform synthetic aperature radar actually benefit from a retrograde orbit.
Okay, but why not launch everything else into a 0° equatorial inclination?
- It takes the least amount of energy (and thus fuel) when you launch at the same inclination as your launch site's latitude. That's not to say you can't launch at a different inclination; it will just take more fuel.
- If you want a 0° inclination with the least amount of fuel, you will need to launch from the equator. That's why the Ariane rocket launched from French Guiana.
- Kennedy Space Center (KSC) is about 29°N. Most satellites launched from there end up with an inclination of about 29°, unless there is reason for a different inclination.
- Canaveral Air Force Base is next door to KSC, and is still used for some military launches. However, many military launches are spy satellites, which (as explained above) benefit from a polar orbit. Thus, a launch complex was built at Vandenburg Air Force Base in California. At a latitude of 35°N, it is more efficient to send spy satellites into polar orbit than Canaveral.
- Sometimes a different inclination is needed to avoid launching over heavily populated areas. Israel launches the Shavit rocket in a retrograde orbit because that takes it over the Mediterranean rather than populated areas.
- Russia launches at Baikonur Cosmodrome in Kazakhstan, latitude 46°N. It usually launches at inclinations in the 50s, to avoid launching over populated areas and so it will orbit/land over Russian territory. Because many of the components and supply missions for the International Space Station originate from Baikonur, the ISS has an inclination of 52°.
Thus, spacecraft vary in how much they change the Earth's angular momentum, and some actually increase it.
- 772
- 1
- 9
- 17
All the existing answers nicely explain the issue, but I'll add some numbers to the discussion:
In 2018, 112 objects have been launched to orbit. Let's assume a typical rocket mass of 500 t and a payload of 10 t (values for the Falcon 9). Of these 112 objects, 30 were launched into high orbits where part of the rocket exhaust may have escaped Earth's sphere of influence (SOI), and four (Elon Musk's Tesla Roadster, InSight, Parker Solar Probe, and BepiColombo) were launched into interplanetary orbits where they and their upper rocket stages, escaped Earth's SOI themselves.
For high orbits, we can assume that about half of the payload's mass leaves Earth's SOI in the form of rocket exhaust. For payloads that are launched into interplanetary space, we can assume that an additional 10 tons are sent in the form of the launcher's spent upper stage.
Assuming that 2018 is a representative year and those guesses are about correct (variations from 0.1 to 10 would be possible),
- The total launched mass is $5 \cdot 10^7\ kg/year$
- The total satellite mass increases by $1 \cdot 10^6\ kg/year$
- The total satellite mass in high orbits increases by $3 \cdot 10^5\ kg/year$
- The total mass leaving Earth's SOI, from both interplanetary launches and rocket exhaust of high-orbit satellites, is $3 \cdot 10^5\ kg/year$
As discussed in the other answers, the mass of satellites that stay inside Earth's SOI has no influence on the distance between Earth and the Sun. The only relevant part is the $3 \cdot 10^5\ kg/year$ that are launched away from Earth.
As you correctly noted, the mass itself isn't relevant, the impulse is, so let's assume that the mass leaves Earth at 10 km/s. The fastest-ever spacecraft to leave Earth was New Horizons at 16 km/s, while a typical Mars transfer takes 6 km/s. Rocket exhaust is typically much slower, on the order of 3 km/s.
We arrive at an impulse of $ 3 \cdot 10^9\ Ns / year $, or an average force of $ 100\ N $.
But in which direction is the force applied? For interplanetary probes the ejection direction depends on your intended destination and transfer plan, while for rocket exhaust from satellites in high orbits it's pretty much random. All in all, I guess that it will pretty much even out. After all, in 2018 two launches were to higher solar orbits and two were to lower solar orbits.
If the force is applied in the same direction in which Earth is moving, it is accelerated and thus lifted into a higher orbit. If the force is applied in the opposite direction, it is decelerated and moves into a lower orbit (closer to the Sun).
The orbital energy of Earth is calculated as $ -\frac{ G \cdot M \cdot m_{Earth}}{2a}$, where G is the constant of gravity, M is the total mass of the Earth-Sun system, and a is the semi-major axis (average distance between Earth and Sun).
The power at which Earth is accelerated or decelerated is $\frac{dE}{dt} = Fv$, where F is the force of acceleration and v is the orbital velocity of Earth. We arrive at
$a(t) = - \frac{G \cdot M \cdot m_{Earth}}{2 \cdot (E_0 \pm F v t)} = - \frac{G \cdot M \cdot m_{Earth}}{2 \cdot E_0} \cdot \frac{1}{1 \pm \cfrac{F v}{E_0} \cdot t} $
$\frac{da(t)}{dt} = - \frac{G \cdot M \cdot m_{Earth}}{2 \cdot E_0} \cdot \frac{da(t)}{dt} (\frac{1}{1 \pm \frac{F v}{E_0} \cdot t}) = - \frac{G \cdot M \cdot m_{Earth}}{2 \cdot E_0} \cdot \frac{\mp \frac{F v}{E_0}}{(1 \pm \frac{F v}{E_0} \cdot t)^2} $.
$\frac{F v}{E_0} \cdot t$ is negligible compared to 1 (about $t \cdot 3 \cdot 10^{-20} / year$), so the formula is simplified to:
$\frac{da}{dt} = \pm \frac{G \cdot M \cdot m_{Earth}}{2 \cdot E_0} \cdot \frac{F v}{E_0} = \pm GM \cdot \frac{m_{Earth}\cdot v}{2 \cdot {E_0}^2} \cdot F = 1.8 \cdot 10^{-18}\ \frac{\frac{m}{s}}{N} \cdot F$.
So the result on Earth's distance from the Sun is $\pm 1.8 \cdot 10^{-16}\ m/s = \pm 5 \cdot 10^{-9}\ m/year$, assuming that everything is ejected in the same direction.
- 181
While rockets seem huge, they are mostly fuel. Most of the fuel is burned up in the atmosphere, and never leaves Earth. The boosters usually return to Earth, so only a relatively small payload remains in orbit, or leaves orbit outward.
- 8,591
The most important thing to grasp, as given in other answers, is the sheer difference of scale between the amount of stuff we have launched into space and the amount of planet we have. According to this previous answer we've launched on the order of tens of millions of kilograms. The mass of the planet is on the order of millions of millions of millions of millions of kilograms.
The other part of the question is about why removing this mass doesn't affect Earth's orbit. A, possibly surprising, fact is that even if you decreased the mass of the planet by a significant amount you would not actually change its orbit. That is because mass comes in numerators and denominators in the relevant equations, and cancels out.
You mention "then gravitational attraction between earth and sun must decrease". That is true. If you halved the mass of the Earth, you would get half the gravitational force on it. However, because force is mass times acceleration, when you halve force and you halve mass, you are left with the same acceleration. The other fact is that the momentum of the Earth decreases when this mass decreases. Again that is true: momentum is proportional to mass times velocity. Once again though, that does not mean that it's going any slower. There is just less of it going as fast as before.
Fundamentally, orbital radius is a function of tangential velocity and centripedal acceleration, and neither of those has changed. Therefore even if we had launched an impossibly huge proportion of the planet (assuming we put it in orbit or disperse it equally in all directions) that wouldn't cause the planet to orbit further from the sun.
- 381
The amount of debris we are sending is so small in comparison to the total mass of the Earth, it is probably less than the error involved in measuring the total mass....
So, any change in angular momentum will be "lost" due to the errors involved.