Equivalence Principle: Why is sitting in space the same as failling in a uniform gravitational field

Question

The equivalence principle states that no experiment can determine whether one is being accelerated or if there is gravity present. This is insightful and intuitive.

However, I was sort of surprised. It is commonly stated that a person in free-fall is weightless, however, if a person was just floating around in empty space (free from any other bodies of mass) they would also feel weightless. This is confusing because that means that having gravity accelerating you and having no force at all are the same?

Why is it that one cannot distinguish free fall in a gravitation field from floating? Intuitively they seem to be different things because there is acceleration in free fall.

Answer 1

The person in free fall near the earth will surely know what weight feels like when they hit the ground! ha ha.

The thought experiment holds in small neighborhoods and small time intervals relative to some standard.

Also, in this thought experiment the observer is isolated from their environment and cannot see out of any windows to determine if things are falling or moving relative to them.

What this basically means is that if you are floating in space inside a box and the box is suddenly accelerated in some direction with 9.8m/s^2 you will hit one of the walls and be able to stand on it feeling the same as if you were on the ground. Einstein asserts that no experiment can determine this scenario from that of being in the presence of a source of gravity that produces an acceleration of 9.8m/s^2 (nothing magical about 9.8 but it's our neighborhood so we know what it feels like).

The feeling of weightlessness is, again, relative. When you are falling you certainly know gravity is at work. If you've ever been sky diving you know damn well. But here you have some relative motion to observe, you are not isolated. We "feel" our weight when we stand on the ground because we feel the normal force of the ground against our feet!

In feel fall the fluids in our body would rise up and fill all our cavities, rather than settle "down" at the "bottom". This is experienced by astronauts in the famous Vomit Comet, a freely falling aircraft used to train astronauts in weightlessness.

Answer 2

There is no place in the known Universe where you can be “floating around in empty space (free from any other bodies of mass)”. There are always other bodies, and you’re never free of them. Even galaxies fall.

So there’s no distinction here to draw: freely floating is just how freely falling looks to the floater.

Answer 3

I'm not a physicist, I just like physics, so don't blindly believe in what I'm going to say.

I think that the two situations are identical because in both cases: First: The observer alone in deep space, and Second: The observer in free fall, the observer's gravitational field is distributed spherically and symmetrically around each part of he (observer). To better understand this mechanism, think that if a force is applied to the observer (in deep space) as if attempting to separate the observer from its own gravitational field, in this case the observer notices the effect of this force and the respective acceleration, because in this case the observer remains slightly ahead of the distribution of his gravitational field, which "tries" to accompany he to maintain spherical symmetry.

Therefore when this force ceases the gravitational field returns to have spherical symmetry. This symmetry to which I refer is the distribution of the field of gravity around each particle that makes up the body of the observer.

This is because the body of the observer has local presence, while its gravitational field is infinitely extensive. It is this extension that prevents the immediate reaction of the field.

In the Second case: When the observer is in free fall, his gravitational field is equally distributed spherically and symmetrically around each particle of his body, because the larger field that causes the free fall attracts equaly and simultaneously, the observer and his own extensive field, thus secured the spherical symmetry.

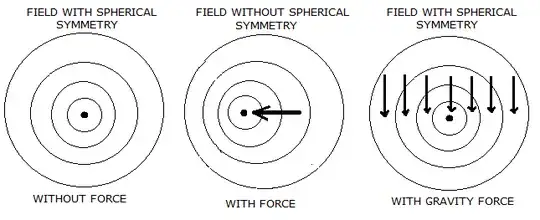
Therefore, the equality between the two situations is justified because in both cases the distribution of the gravitational field, around each respective particle that makes up the observer's body, is symmetrically spherical.

Sorry for my English.