In answers to two other questions on this site:
Mercury's Orbital Precession in Special Relativity
and
Do 2-body elliptic orbits precess in special relativity?
it is stated that special relativity could account for one sixth of the "anomalous perihelion shift" of Mercury and other planets.
If I insert the "relativistic mass" (I know people hate that term) on both sides of Newtons equation for gravitational acceleration you first have:
$$\frac{d(m\gamma\bar{v})}{dt}=-\frac{GMm\gamma}{r^2}\hat{r}\tag1$$
and you end up with:
$$\frac{d\bar{v}}{dt}=-\frac{GM}{r^2}(\hat{r}-\frac{v^2}{c^2}(\hat{r}\cdot\hat{v})\hat{v})\tag2$$
($\hat{r}=\bar{r}/r, \hat{v}=\bar{v}/v, \gamma=1/\sqrt{1-v^2/c2}$)
This will give you more or less precisely one third of the experimentally found anomalous perihelion shift. (I checked this out by numerical integration, I do not have an analytical solution)
I guess it can be argued whether adding a "relativistic mass" in the form used in special relativity to the expression for gravitational acceleration by Newton constitutes "special relativity" or not.
Still using this method you get one third of the anomalous perihelion shift and not one sixth.
Questions:
1. Do SR account for one third or one sixth of the so called anomalous "perihelion shift"?
2. Can you say that one third of the weak field perihelion shift is explained by using the "Lorentz factor" in this way and two thirds are due to effects accounted for in general relativity but not in special relativity?
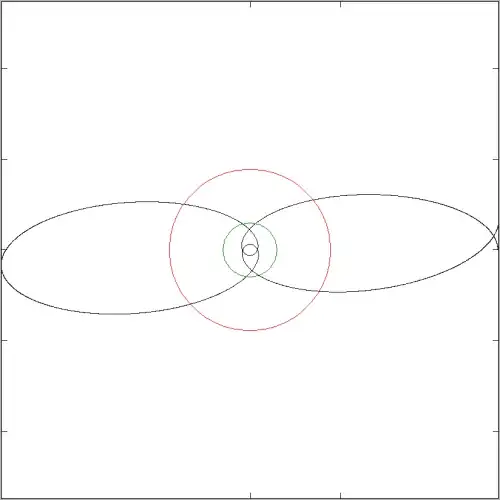
In the strong field limit you get orbits using the expression above that are obviously wrong, but still in the ballpark. The green circle represents the Schwarzschild radius and the red circle the innermost stable circular orbit. In this special case one gets three revolutions between consecutive aphelions.
According to both current answers by Elio Fabri and Pulsar assuming:
$$\frac{d(m\gamma\bar{v})}{dt}=-\frac{GMm}{r^2}\hat{r}\tag3$$
which results in:
$$\frac{d\bar{v}}{dt}=-\frac{1}{\gamma}\frac{GM}{r^2}(\hat{r}-\frac{v^2}{c^2}(\hat{r}\cdot\hat{v})\hat{v})\tag4$$
results in one sixth of the experimentally found perihelion shift and is the most SR way to do it based on arguments that you can get (4) but probably not (2) from a Lagrangian approach and that (4) but not (2) is consistent with a "conservative force". It could perhaps be argued that (3) violates the equivalence principle as you have "$m\gamma$" on the left side of the equation but only "$m$" on the right side. Note that using (4) we no longer have $v=\sqrt{GM/r}$ for circular orbits as is true in both classical mechanics and general relativity (in Schwarzschild coordinates using coordinate time at least) and using (2). Instead, for circular orbits, we end up with:
$v\sqrt{\gamma}=\sqrt{GM/r} \tag5$
It is a bit strange if you get the correct orbital velocity in both GR and classically but not in SR, if we assume (4) is the correct SR expression.
I plotted an example of a strong field orbit using (4) below. The extra factor of $1/\gamma$ appearing in (4) but not in (2) weakens the gravitational acceleration at high velocities and thus gives less perihelion shift. The kinds of orbits one gets using (4) instead of (2) looks less like what is expected from GR.