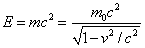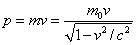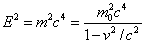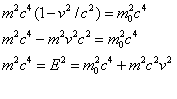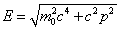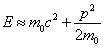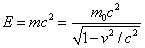Let's consider
$$E_f^2=(mc^2)^2+(pc)^2$$
where the $mc^2$ is the rest energy due to the rest mass -- in Finnish "lepomassa".
$$ \sqrt{(mc^2)^2+(pc)^2} - mc^2~=~(\gamma-1)mc^2$$
is the kinetic energy due to the movement because of momentum $p=\gamma mv$.
Now where is potential energy if $E_f=\gamma mc^2$ is the total energy?
The formula you quote does not contain the potential energy, it is valid for a free particle (i.e. a particle which is not affected by external potential). You can link it to classical mechanics by evaluating it for small values of $p$ (more precisely: $ p \ll c$):
$$ E = \sqrt{\left(mc^2\right)^2 + p^2 c^2} = c \sqrt{m^2c^2 + p^2} = \cdots $$
$$ \cdots = mc^2 \sqrt{1 + \frac{p^2}{m^2 c^2}} \approx mc^2 \left( 1 + \frac{p^2}{2 m^2 c^2} \right) = \cdots $$
$$ \cdots = \text{constant} + \frac{p^2}{2m} = \text{constant} + \frac{1}{2} m v^2 $$
Here we see that the relativistic formula in the non-relativistic (i.e. small speeds) limit reduces to the classical one, apart for a constant energy associated to the mass of the object, which is a purely relativistic concept.
The constant is, by the way, $mc^2$, and that's explains why the formula $E=mc^2$ is so famous, as it catches one of the most astonishing concept of special relativity: an object just for existing and having mass $m$, has an energy $E=mc^2$, i.e. the rest energy.
The energy in your equation is for a free rigid body in the absence of a potential. We can see this if we start with a Lagrangian with a scalar function, $\Phi(q)$, and remember $\gamma$ is a function of $\dot{q}$, $$ L=T-V=-\gamma^{-1} (\dot{q}) \, mc^2-\Phi(q) $$ Then if we find the momentum $$ \pi=\frac{\partial L}{\partial \dot{q}}=\gamma^{-2}\frac{\partial \gamma}{\partial \dot{q}}mc^2=\gamma m\dot{q} $$ Thus, the Hamiltonian, $$ H=\pi\dot{q}-L=\gamma m\dot{q}^2+\gamma^{-1} (\dot{q}) \, mc^2 + \Phi(q) $$ which gives after factoring out $\gamma mc^2$, $$ H=\gamma mc^2(\frac{\dot{q}^2}{c^2}+\gamma^{-2})+\Phi(q)=\gamma mc^2+\Phi $$ The first term is the one you like, and the second one is the potential energy if you'd like.
In the standard formula given in the question posed, the potential energy is zero. The formula applies to a free particle only.
For a charged particle of charge Q in an electromagnetic field, the correct formula for the total (kinetic plus potential) energy is $$E= c\sqrt{(mc)^2 + (p+QA)^2} -QA_0,$$ (e.g., $Q=-e$ for an electron) where $A$ and $A_0$ are the space (vector) part and the time (scalar) part of the electromagnetic gauge potential. Here $-QA_0$ is the potential energy.
For gravitational forces, the correct formula is given by the solution $E=p_0$ of the equation $G(p,p_0)=const$, where $G$ is a Lorentzian quadratic form (whose coefficients define the metric tensor) in the space part $p$ and the time part $p_0$ of the relativistic 4-momentum vector. Here a potiential energy can be identified only in a nonrelativistic limit.
If both kinds of forces are present, the correct formula is given by the solution $E=cp_0$ of the equation $$G(p+QA,p_0+QA_0)=0$$. Specializing the quadratic form to $G(p,p_0)=const(p_0^2-p^2)$ gives the above formula.
Potential energy is the property of a system, not of individual particles. Even in classical mechanics this is true. The usual way of saying something's potential energy can be seen as an abuse of notation.
So for one particle $E=\gamma m c^2$ does not include potential energy, but the energy of the total system (a point charge and a capacitor, for example) include the potential energy. The potential energy shifts the rest mass of the system from the sum of the mass of individual components (in addition to the effect of relative motion).
Another viewpoint is that potential energy is stored in fields, so the shift in rest mass is due to energy of the field.
The total energy is the rest energy plus the kinetic Energy, $E_f=γmc^2$, we can assume the term PC goes to zero and therefore potential energy is then the total energy of the object at rest. To present clarity to your question inspires us to look beyond the rest energy $E=m_0c^2$ of the object and notice that as the momentum increases the kinetic energy of the object becomes much more important than the rest energy.
Let's look at Energy and Momentum in Lorentz Transformations
Source of following : From Michael Fowler, University of Virginia
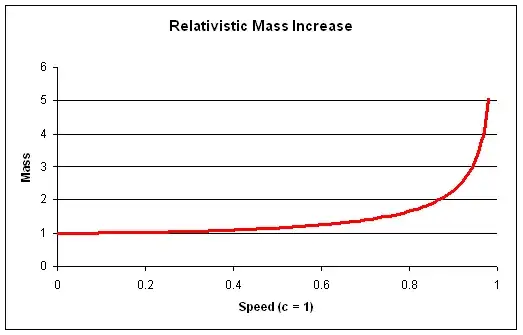
We have a formula for the total energy E = K.E. + rest energy,
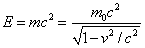
so we can see how total energy varies with speed.
The momentum varies with speed as
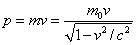
How Does the Total Energy of a Particle Depend on Momentum?
It turns out to be useful to have a formula for E in terms of p.
Now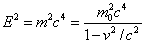
so
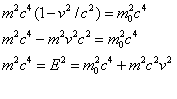
hence using p = mv we find
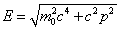
If p is very small, this gives
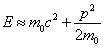
the usual classical formula.
If p is very large, so $c^2p^2$ >> $m_0^2c^4$, the approximate formula is
$E=cp$
{My note added here. As $p$, the momentum is very large in your equation and as $mc^2$ becomes negligible and we can essentially drop it from your equation $E_f^2=(mc^2)^2+(pc)^2$ and are left with $E^2=(pc)^2$ & {drop $(mc^2)^2$} and left with $E=pc$}
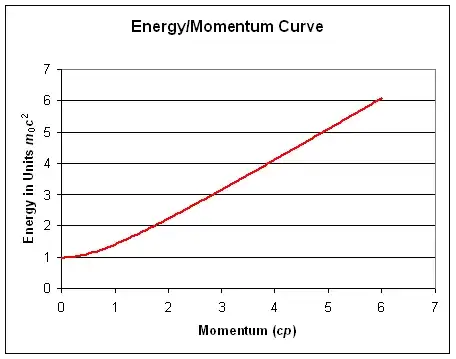
The High Kinetic Energy Limit: Rest Mass Becomes Unimportant!
Notice that this high energy limit is just the energy-momentum relationship Maxwell found to be true for light, for all $p$. This could only be true for all $p$ if $m_0^2c^4=0$, that is, $m_0=0$.
Light is in fact composed of “photons”—particles having zero “rest mass”... The “rest mass” of a photon is meaningless, since they’re never at rest—the energy of a photon
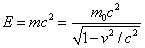
is of the form $0/0$, since $m_0=0$ and $v=c$, so “$m$” can still be nonzero. That is to say, the mass of a photon is really all K.E. mass.
In closing ... We will really need to think hard on this as we stop photons for quantum computing.
But to answer your question Total Energy = potential Energy + kinetic Energy
Since $pc$ = the kinetic energy and as $p$ goes to zero the Total Energy = potential energy and therefore all that is left is $m_0c^2$, the rest energy. I hope looking at the momentum from both a zero to large value gives you a clearer understanding why the rest energy is the potential energy.
In reference to your question. Now where is potential energy if $E_f=\gamma mc^2$ is the total energy?
$E_f^2=(m_0c^2)^2+(pc)^2$
$E_f^2=(m_0c^2)^2+(pc)^2$
$E_f=\sqrt{(m_0c^2)^2+(pc)^2}=\gamma mc^2$
$(\sqrt{(m_0c^2)^2+(pc)^2})^2=(\gamma mc^2)^2$
$(m_0c^2)^2+(pc)^2 = (\gamma mc^2)^2$
$(m_0c^2)^2=(\gamma mc^2)^2-(pc)^2$
$m_0c^2 = \sqrt{(\gamma mc^2)^2-(pc)^2}$
Finally the potential energy or rest energy is as expected the total energy $\gamma mc^2$ less the kinetic energy. Perhaps what you are looking for is putting the potential energy in terms of total energy and momentum. {Please note it was important to qualify the masses into $m_0$ rest mass and $m_v$ a moving mass of the momentum. The rest mass will be a constant while the mass of the momentum term will vary as the velocity changes and extremely so as v->c}
$m_0c^2 = (\gamma mc^2)-(pc) = (\gamma mc^2)-(m_vvc)$
Most of the given answers here are "not even wrong" because they address an irrelevant point. Obviously we're considering an object that is not moving in an external potential, so the question is how to interpret the difference of the total and the kinetic energy. The quantity $m c^2$ is the sum of the potential and kinetic energy of the system comprising of only the object in its rest frame. The total energy in a frame where it has a velocity of $v$ is $\gamma m c^2$, the kinetic energy of $(\gamma - 1)m c^2$ refers to only the kinetic energy if its center of mass motion.
Note that splitting up the internal energy of $mc^2$ in kinetic part and a potential part is arbitrary. Take e.g. the van der Waals interaction between atoms. the total energy of two atoms a distance $R$ apart depends on $R$, minus the derivative w.r.t. $R$ is the van der Waals force. While we can call this energy the potential energy of the two atoms, one can split it up in a kinetic part and a potential part when considering the electrons in both atoms.
