I was doing an exercise in physics and I noted that the angular acceleration was negative. What does that mean?
1 Answers
It's simple: the body with negative angular acceleration has a decreasing angular velocity (or an increasing negative angular velocity).
Mathematically, it's simple: if $\omega$ is the angular velocity (and $\omega_0$ is the angular velocity at $t=0$, then it follows the relation $$\omega=\omega_0+\alpha\times t$$. If $\alpha$ (angular acceleration) is positive, the angular velocity increases, and decreases if $\alpha$ is negative. If the angular velocity was negative, then the exact opposite happens.
Which begs the question: what does it mean to have angular velocity negative?
To answer that, let me first explain this situation with linear velocity/displacement, since it may lead to a much better understanding of the general concept of negative <whatever>:
What does it mean for linear displacement to be negative?
Let's look at a one-dimensional case1. Imagine a point particle living in this coordinate system:
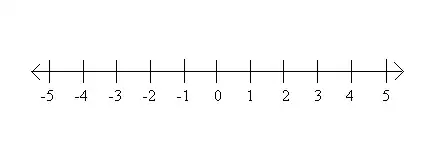
Let's say it moves from $x=1$ to $x=2$. Here, the displacement is $+1$. Why? Because $s=x_2-x_1=2-1=+1$ ($s$ is displacement). If it moved from $x=4$ to $x=3$, displacement would be negative. Basically, if the displacement vector2 points along the positive $x$ axis, then the displacement is positive, else, negative. Which direction s the positive $x$ axis is up to you, as long as you use the same one consistently while analyzing the same situation.
OK, so what does it mean for linear velocity to be negative?
Simple. This means that the body moves along the negative $x$ axis. $s=vt$, so a body with positive net displacement will have its displacement reduceds time increases a, while one with negative displacement will go further negative (so, it goes further to the left in the coordinate system above)
So what about negative linear acceleration?
By now it must be obvious to you that this means an "acceleration" along the negative $x$ axis. Think of it as the body getting a "push" in this direction.
If the acceleration has the same sign as velocity, then it is accelerating (speeding up). If it has an opposite sign, it is decelerating (slowing down, eventually going in reverse).
Alright. How does this relate to angular situations?
In the angular case, it's essentially the same thing. We arbitrarily choose a direction to be positive, and its opposite automatically becomes "negative". We generally take clockwise as positive.
So, angular displacement($\theta$) in the clockwise direction is positive. Negative angular velocity($\omega$) means that the particle is revolving anticlockwise. Thus, negative angular acceleration($\alpha$) is a "push" in the anticlockwise direction. If $\alpha$ and $\omega$ have the same sign, the body will speed up, else slow down (and eventually go in reverse).
Actually, $\omega$ and $\alpha$ can be looked at as vectors as well. They point perpendicularly to the plane of rotation, and the direction (up or down) is determined by the right hand thumb rule -- if you are looking down at the plane and the vector points towards you, the direction corresponding to the vector is clockwise.
Looking at it this way, we have a case similar to linear motion--vectors adding and subtracting.
1. In higher dimensions, these quantities cannot be given a sign, so there is no point talking about negative linear displacement/acceleration.. 2. This vector has a length equal to the scalar displacement, and points in the direction of net movement.
- 19,167
- 6
- 64
- 104