5

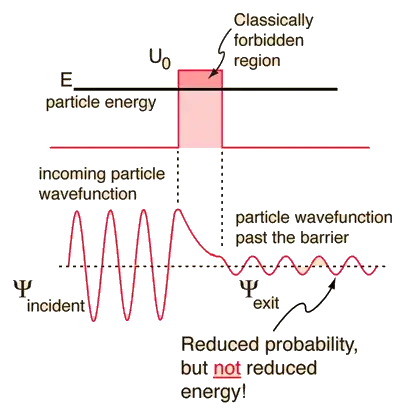
According to my understanding quantum mechanics, the probability of any particular particle in the universe being at any specific location in the universe is very small but never actually becomes zero. Thus, a little bit of all of us is everywhere.

Let's assume I suddenly quantum tunneled from sea level to the top of Mount Everest. That jump represents a net increase in energy/mass for Earth, which would violate the first law of thermodynamics. My calculations indicate it would have increased the mass of Earth by around 0.0858657µg, unless it is somehow offset some other phenomenon.

It seems implausible to me that energy conservation for a closed system could actually be violated, so how would that net increase in energy/mass be accounted for?

Or does the fact that such a scenario by definition represents such a significant decrease in the entropy of the system mean that an increase in mass should be the expected result?

Robert Quattlebaum
  • 151

1 Answers1

4

Here are the basics of quantum tunneling:

barrier penetration

Note, the energy level of the particle in the above simple example does not change.

This holds true for all tunneling scenaria:

There should exist wave functions $Ψ$ , i.e. solutions for the quantum mechanical equations applicable to the problem where the specific boundary conditions have been applied. Then the $Ψ^*Ψ$ computation will give the probability for the particle to be found outside the barrier.

Energy conservation is a universal rule that is incorporated in all wavefunction calculations. Thus the probability of finding the particle in a different energy level than the one in the solution is zero, no matter how complex the solutions and the boundary conditions.

anna v
  • 236,935