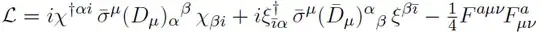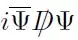$U(N)$ & $SU(N)$ : What's the conceptual difference in Gauge Theory?

Question

I know the mathematical difference that one means $ absolutevalue(det) = 1$ and one means det = 1 (rotation) and that ones the subgroup of the other and so on.

But:

has a local/gauged $SU(3)$ colour gauge symmetry and global $U(2)\times U(2)$ flavour symmetry. This is the Weyl-field lagrangian for $u$ & $d$ quarks.

I'm confused why it should be a $U$ or a $SU$ symmetry, since both are unitary: $1=U^{\dagger} U$ makes bilinears like

invariant. So you should choose $U$ as the symmetry group, since its bigger. Do gauged/local symmetries have to be $SU$ and global can be $U$? Or what's the point here?

EDIT: I think that's the reason, since a local $U(N)$ transformation would need a local absolute value

$a(x)\exp(i\theta^{a}(x) t^{a})$

and then you need to use the product rule for differentiation and that makes things complicated.

Answer 1

$U(3) \sim SU(3)_{color} * U(1)_{B-L}$ has been considered in some versions (e.g. as components of Pati-Salam's SU(4)) of Standard Model extension. If $SU(3)_{color}$ and $U(1)_{B-L}$ are considered as direct product, then they can have different coupling constants. Otherwise (if embedded in $SU(4)$) they share the same CC.