Addendum 1 (Illustration added at the beginning):
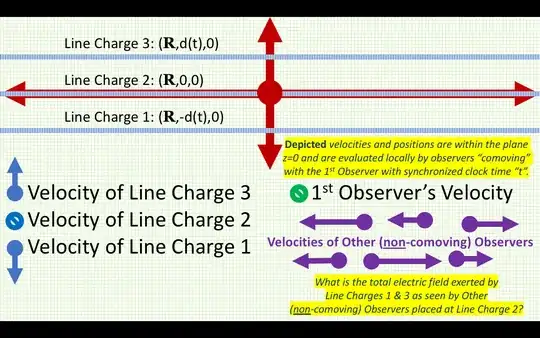
Suppose I had 3 identical parallel line charges parallel to the x-axis of infinite length in the same geometric plane.
The first and third line charges are equidistant from the second.
Now suppose I have a series of observers that have different velocities which vary only along the x-axis (i.e. differences in the x-component of velocity only).
For our first observer, the "center of charge" is stationary, and for the rest of the observers the "center of charge" is moving at some velocity directed along the x-axis. The first observer would observe no component of the electric field directed along the x-axis.
However, the others would observe such electric fields directed along the x-axis.
How do we ensure there is no acceleration of the second line charge despite the electric field exerted on it in the x-direction? Is its momentum affected due to the varying "electric potential" therefore "mass" in some compensating way, ensuring no acceleration, as in (mv)' - m'v = mv' = 0?
Addendum 2 (Added complementary information):
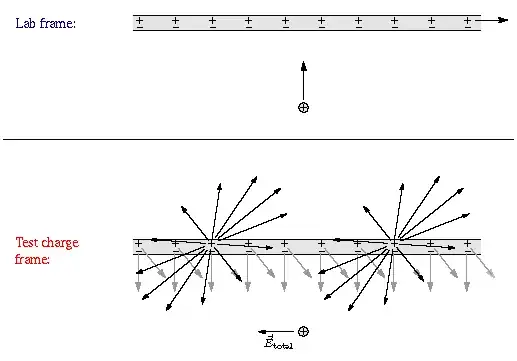
One should consider how a neutral wire with an electric current can be represented by the superposition of two line charges with equal and opposite linear charge densities while having different velocities. Notice that in the bottom half of the illustration below labeled "Test charge frame:" (in red) it shows an electric field with a component parallel to the wire that exists because the positive charges contribute to it and yet the negative charges do not negate that contribution. From http://physics.weber.edu/schroeder/mrr/mrrtalk.html
I've included information about this because some may doubt that electric field components in the x-direction are seen by observers having different component velocities in the x-direction than those of the line charges.