Collision of block and a spring system kept at rest

Question

A body of mass $m$ moving with velocity $v$ collides with a system of 2 blocks of each mass $m$ connected by a spring of spring constant $k$. All the three lie on the same plane (1D collision). There is no friction anywhere.Do the spring compress? . If yes then why? To compress or elongate a spring equal and opposite forces should be applied to opposite ends, then how could the spring compress. Please explain

Answer 1

It seems you tacitly set a colinear collision, if not let me know to modify the answer.

The spring will compress in a variety of modes.

-If the collision is elastic, the moving block will stop entirely after it hits the stationary block and give all its momentum (Newtons system of balls and cradle ) to stationary block and then that stationary block starts to move back with speed v and this will compress the spring and start to push the last block back. This will start a free vibration in the system of the spring and two blocks which will gradually slide away while vibrating.

-If the collusion is not elastic there will be some loss of kinetic energy of the moving block and it may recoil back while pushing the second block back and compressing the spring, or depending on the stiffness and length of spring it may become one with the two blocks and move and with them at least for the compression part of the vibration.

Answer 2

Do the spring compress?

Yes.

There is no friction any where. If yes then why?

Because the spring itself and the mass on its end have some inertia.

To compress or elongate a spring equal and opposite forces should be applied to opposite ends, then how could the spring compress.

No, that is wrong. If a one sided force is applied to a spring, it will accelerate. An accelerated spring will compress, because each part of the spring has inertia/mass. I have answered a somewhat similar question here.

Answer 3

Let's assume the before the collision took place the mass $ m_{1} $ (which is just a designation for the block which collides with the other two blocks) had a velocity say $ v $ it can be assumed that the coefficient of restitution is $ e $ such that $ 0≤e≤1 $ now using the conservation of momentum and equation of restitution we would have $ v_{2} = \frac { ( e+1)v}{2} $ , where $ v_{2} $ denotes the velocity of the mass which initially collides with the moving block . With this now we shift to consider the centre of mass frame of the two blocks connected by the spring . In this frameas in absence of external forces $ V _ { cm } $ cannot change and hence we have :- 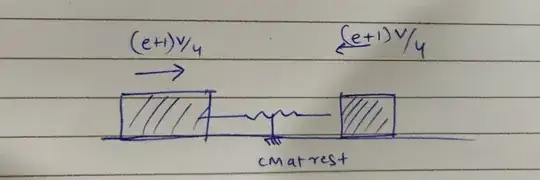using this we can see that the springs must compress so as to conserve the energy of the system .