Is there an intuitive explanation why it is plausible that the gravitational force which acts between two point masses is proportional to the inverse square of the distance $r$ between the masses (and not only to the inverse of $r$)?
5 Answers
Richard Feynman explains it wonderfully in his lectures on the "Character of Physical Law". You could have a look at this video.
One way to see it is that the inverse square law just is. There were experiments done to determine how one mass affects the other and then the result was that the force between them varies as the inverse square of the distance between them. But clearly that is neither intuitive nor obtained from "first principles". In other words, once we have the experimental data, who is there to explain it?
You can see that it has to be an inverse square law by symmetry. The other arguments for this question involve gravitons, but the argument works just as well even for fields.
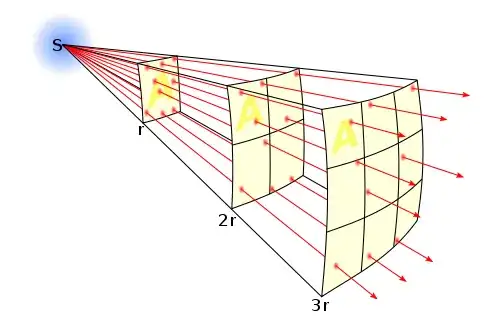
From the image a general idea of the argument can be seen. The argument goes like so:
If you consider a point mass in space, and then claim that it has a "gravitational field" around it, then from the law of conservation of energy the energy of the field has to be conserved in all space. But since the source of the field is a point mass, it is also clear that the field has to be spherically symmetric (since from every region around the point mass, the point mass looks the same). So if we consider a spherical region around the point and measure the total field passing through that surface (called the flux of the field) and then consider another spherical region with a larger radius and measure the field passing through that surface, the total field through both spherical surfaces must be equal.
But the surface area of the sphere goes up as $4\pi r^2$. Therefore for the flux through both spherical surfaces to be the same, the field has to go down as $1/r^2$.
- 3,767
- 2
- 23
- 38
If you think of the gravitational force carried by particles like gravitons, the flux of these force-carriers would fall off like $1/r^2$, just like photons from a point source. And that is due to the fact that they are spread out over a sphere with area $4\pi r^2$.
- 3,811
Inverse-square laws are completely geometry-based.
Let us assume a point source. This point source may emit anything such as Gravity, Light, Sound, Radiation, etc. One thing to note in these point sources - They spread their influence equally in all directions (approaching infinity) without limit to their covered range.
For instance let us assume light. It emerges as spherical wave-fronts from this point source. Taking a slice off this sphere and when projected in a perspective view, we'd get a square matrix of order of $\text{your distance}$. If you take $2 m$, then it'd be in a $2\times 2$ matrix which has $4$ elements which basically takes the square. If we look - into with our goggles somewhat, we'd see that these spherical wave-fronts spread in the form of $\text{your distance}$ as their radii $r$.
We know that the actual source strength of gravity is $4\pi GM$ whereas the surface area traversed by the spheres is $4\pi r^2$ and it results in the gravitational field intensity $$I=\frac{GM}{r^2}$$
- 9,178
Two answers come to mind (I assume this explanation is to be provided to non-specialists and non-would-be-specialists, as there is intuitive in the question):
Argue by "heavy body and satellite problem" that other values make no sense (of course this can rule out $r^{-1}$ but not $r^{-1.9992}$). Data for comparison - how long is the Martian year (or year on Pluto).
Say that the body emits gravitons in all directions and the total flux of gravitons has to be preserved which implies $r^{-2}$.
The second "argument" gives -2 power, but also is an "proof" by a unverified conjecture. Nevertheless it requires no calculation, therefore qualifies for intuitive.
No, there is no intuitive explanation why the gravitational force which acts between two point masses is proportional to the inverse square of the distance $r$ between the masses. All geometrical reasonings involve surfaces, not the point-like bodies, so they are too speculative.
- 14,125