1

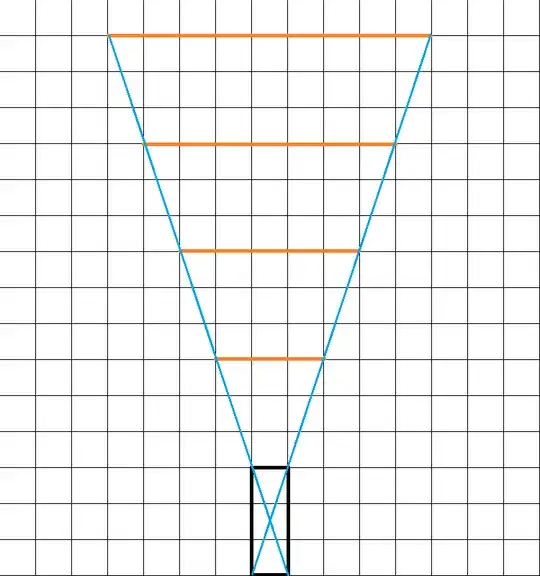
I'm aware of the usage of special lenses known as Telecentricity but these are still, ultimately, lenses, and suffer from loss of focus at a certain range:

It is a common misconception that Telecentric Lenses inherently have a larger depth of field than conventional lenses. While depth of field is still ultimately governed by the wavelength and f/# of the lens, it is true that Telecentric Lenses can have a larger usable depth of field than conventional lenses due to the symmetrical blurring on either side of best focus.

We already have sensors that can detect color so what's to stop us from putting one of those sensors at the end of a very long, thin tube coated in Vantablack allowing light to enter only from directly ahead of the tube, generating a "pixel", which, with tens of thousands of these sensors in a grid formation, could seemingly create a truly orthographic image of whatever light is directly in front of the sensors. In space, while it would be similar to looking at the universe through a pinhole, perhaps a 5 meter x 5 meter square visible at a time with millions of the sensors, it seems like such a tool would still be useful.

It seems like you would then be able to see 25 feet at a time of any object at any distance, in color, with good clarity at true-size. But that sounds too good to be true. What factors of physics would make such a device unrealistic?

J.Todd
  • 1,841

1 Answers1

2

For the sake of simplicity let's say the tubes have a square profile. The side of this square is $a$, so the area of the sensor is $a^2$, the length of the tube is $L$, the distance from the sensor-end of the tube to the surface of the observed object is $d$. Even ignoring diffraction, at $d=2L$ you will have the sensor collecting light from an area of $9a^2$, at $d=3L$ you have the sensor collecting light from an area of $25a^2$, at $d=4L$, the area is $49a^2$ and so on, with the obvious equation being: $$A_{collected} = (2\frac{d}{L}-1)^2a^2$$

Here is an image to help you visualize. The black rectangle on the bottom-middle is the tube, with its width = $a$ and height = $L$, the blue lines represent the line of sight, the orange lines are the areas (at different distances) that contribute light to the sensor. Keep in mind that this is a 2d representation of a 3d system, this is why in the image the closest orange line has length of $3a$, which translates to an area of $(3a)^2 = 9a^a$ (like I said above). Same goes for the rest of the orange lines.Visual aid

To put this into perspective (generously) if $L=100m$, and $a=0.1mm$ looking at the moon each sensor will collect light from an area of more than $5\cdot 10^5m^2$. The overlapping of the areas, each sensor collects, would be awful. You would probably see just a smudge. At this point multiple tubes are just pointless, as you would need an array of ridiculous size for the sensors that are furthest away to collect anything meaningfully different.

Looking at Alpha Centauri A (The largest star in the nearest star system, other than the Sun) each sensor will collect light from more than $5\cdot 10^{21} m^2$. That is orders of magnitude larger than the star's area.

You can see why such a devise fails, even looking at relatively close objects.

K. Kirilov
  • 629