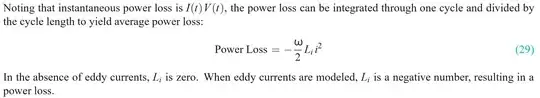Today I came across with Complex Capacitances and Inductances for the first time: $$L(j\omega)=L_{real}+jL_{imaginary}$$ $$C(j\omega)=C_{real}+jC_{imaginary}$$
So I started looking at their meaning. Let's start with the inductors.
Inductors:
I found this article, that states (pages 7 and 8):
After that, I found that this "Power Loss" is associated with "Core Losses", like hysteresis losses, Eddy/Foucault current losses. So, my first question is:
- If $L_{imaginary}<0$, we have $Power\space Loss >0$, so we have a dissipation of energy by the magnetic core of the inductor due to (according to what the article says) eddy currents;
- If $L_{imaginary}=0$, we have $Power\space Loss =0$, so no eddy current and no energy dissipation;
But, what if $L_{imaginary}>0$ ? Then we will have $Power\space Loss <0$, i. e., the magnetic core will supply power to the circuit! How is this possible? Or is the value of $L_{imaginary}$ somehow restricted by some equation, so that it cannot assume positive values?
(Another way to state this is considering the inductor impedance:$$Z_L=j\omega L=j\omega\cdot(L_r+jL_i\ )=-\omega L_i+j\omega L_r\ \ $$ The imaginary part of $L$ contributes to the real part of inductor impedance. This contribution is given in the form of a frequency dependent resistance $-\omega L_i$. So, if we have $L_i>0$ then $-\omega L_i<0$, a negative resistance!)
Capacitors:
I found this article. It states that (page 2) $C_{imaginary}$ is associated with dielectric loss.
Another source states that this dielectric loss can be by Joule's heating effect, hysteresis losses and dielectric absorption. I guess we can model this dielectric loss in a analogous way to the losses in the inductor core: $$Power\space Loss=-\frac\omega2 C_i v^2$$
Thus, a similar question arises:
- If $C_{imaginary}<0$, we have $Power\space Loss >0$, so we have a dissipation of energy by the dielectric;
- If $C_{imaginary}=0$, we have $Power\space Loss =0$, so no energy dissipation;
But, what if $C_{imaginary}>0$ ? Then we will have $Power\space Loss <0$, i. e., the dielectric of the capacitor will supply power to the circuit! Again, how is this possible? Or is the value of $C_{imaginary}$ somehow restricted by some equation, so that it cannot assume positive values?