2

We were reading about atomic structures and bond making and my teacher told me that when two atoms are fused or when they make bond, two orbitals are formed. 1-Bonding Molecular Orbital & 2- Anti-Bonding Molecular Orbital. I can't figure it out why these two orbitals are created?

I searched on internet and now stuck at the point that according to Pauli's Exclusion Principle, no two electrons can have same four quantum numbers. That's why two orbitals are formed, I thought two orbitals for each electron but I came to know that Anti-Bonding Molecular Orbital is completely empty having high energy, means there is no electron or anything in it and now I am confused in it.

Can anybody explain this to me so I can explain to my other classmates?

Emilio Pisanty
  • 137,480
devWaleed
  • 346

1 Answers1

4

Your teacher is referring to the LCAO approximation as a way of calculating molecular orbitals.

Suppose you bring two hydrogen atoms together i.e. create a hydrogen molecule. To calculate the electronic structure you need to solve the Schrodinger equation, but even for something as simple as the hydrogen molecule the Schrodinger equation is too complex to solve analytically. To make progress we need to use some approximate method.

When the hydrogen atoms are a long distance apart we know the electronic structure is simple the wavefunction of a hydrogen atom, $\psi_H$. So in the hydrogen molecule it's a reasonable guess that the H$_2$ wavefunction might look a bit like a combination of the two atomic wavefunctions. We could add or subtract the atomic orbitals to give:

$$ \Psi_{H_2}^+ \approx \frac{1}{\sqrt{2}} \left( \psi_{H_a} + \psi_{H_b} \right) $$

or:

$$ \Psi_{H_2}^- \approx \frac{1}{\sqrt{2}} \left( \psi_{H_a} - \psi_{H_b} \right) $$

If you have a look at the molecular orbital diagram for hydrogen:

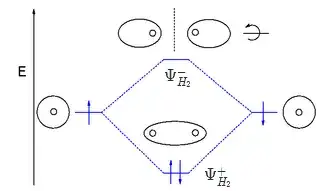
Splitting

the wavefunction $\Psi_{H_2}^+$ is lower in energy than the atomic wavefunction because it increases the electron density in between the protons where they are attracted to both protons. By contrast $\Psi_{H_2}^-$ is higher in energy because it reduces the electron density in between the protons. Hence it's said that the two atomic orbitals split as the hydrogen atoms approach each other to give bonding and anti-bonding molecular orbitals.

But I must emphasise that this is a hand waving approach. In many circumstances it can give you a rough idea of what's going on, but it's a crude model and only useful in simple cases.

John Rennie
  • 367,598