We know that in a Kerr Black Hole the singularity is in the form of a 1 dimensional ring. If we have a 25 solar mass black hole, how big would the Kerr Ring be, width wise?
Also, I read the Wiki on Kerr Black Holes, is the ring shape due to centrifugal force?
The geometry inside a Kerr black hole is pretty crazy. The ring singularity doesn't have a proper "radius" (or "diameter"), nor does any other concentric circle in the equatorial plane. However, a concentric circle in the equatorial plane (herafter just called a "circle") does have a proper circumference. The ring singularity itself doesn't, but other circles do, so we can pick some other special circle and use its proper circumference to characterize the "size" of the black hole.
By proper circumference, I mean the proper (coordinate-independent) distance around the circumference of the circle, computed using the spacetime metric. From now on, "circumference" means proper circumference.
With that in mind, here's one way to answer the question. Let $G$ and $c$ be Newton's constant and the speed of light, respectively. For any Kerr black hole with total mass $M$, the appendix shows that the event horizon has circumference $K_\text{horizon}$ given by $$ K_\text{horizon}=\frac{4\pi GM}{c^2} \tag{1} $$ in the equatorial plane, regardless of how fast the black hole is spinning, with one caveat: if it's spinning too fast, then it doesn't have an event horizon at all. But as long as its angular momentum $J$ satisfies the inequality $$ J<\frac{GM^2}{c}, \tag{2} $$ then an event horizon is present, and its equatorial circumference $K$ is given by equation (1).
We might prefer a notion of "size" that does depend on how fast the black hole is spinning. There are a few natural options. Here I'll describe one that is relatively close in spirit to the one requested in the OP, and it also highlights how crazy the geometry is inside a Kerr black hole.
Consider the continuous family of concentric circles in the equatorial plane, starting with the (outer) even horizon and progressing inward toward the ring singularity. Four such circles are depicted here:
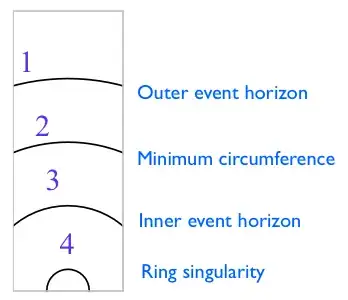
Surprisingly, the proper circumference reaches a minimum value at an intermediate circle, shown here as circle $2$. The circumference increases when moving either away from the center or toward the center. In particular, the circumference of the outer horizon (circle $1$) is the same as the circumference of the inner horizon (circle $3$). Continuing inward toward the ring singularity, the circumference continues to increase, becoming "infinite" (undefined) at the ring singulariy (circle $4$). The minimum circumference $K_\text{min}$ (circle $2$) depends on both the mass and spin of the black hole, unlike the equatorial circumference of either event horizon (circles $1$ or $3$), which depends only on the mass. For a given mass $M$ and a given angular momentum $J\geq 0$ satisfying the inequality (2), the minimum circumference is $$ K_\text{min}=2\pi\sqrt{a^2+3(ma^2)^{2/3}} \tag{3} $$ where the quantities $m$ and $a$, both of which have units of length, are defined by $$ m=\frac{GM}{c^2} \hskip2cm a=\frac{J}{Mc}. \tag{4} $$ In terms of these quantities, the inequality (2) is $$ a < m. \tag{5} $$ The circle with the minimum circumference (3) is hidden behind the outer event horizon, but we can still use it to characterize the size of the black hole. In the non-spinning case ($a\to 0$), the minimum circumference (3) shrinks to zero, but the circumference of the event horizon (1) remains the same. In this sense, the minimum circumference $K_\text{min}$ is a better proxy for the (undefined) size of the ring singularity.
If we use the minimum circumference (3) to characterize the size of the black hole, then the question can be interpreted like this: For a Kerr black hole with a given mass $M$, how big can the minimum circumference $K_\text{min}$ be? The answer is $$ \text{max}(K_\text{min})=4\pi\frac{GM}{c^2}, \tag{6} $$ which is obtained from (3) by setting the spin to is maximum value $a=m$ (an extremal Kerr black hole), the borderline case between a black hole and a naked singularity. The circumference (6) is the same as (1), so the maximum "size" of the black hole is the same using either one of these two definitions of "size." Quantitatively, for a black hole with the mass $M=25\times$ the mass of the sun, this circumference is $$ K\approx 466\text{ km}. $$ If we use this to define a "diameter" $D$ by $D=K/\pi$, then the "diameter" would be $D\approx 148$ km.
is the ring shape due to centrifugal force?
Since the spacetime metric is undefined on the ring singularity, this question doesn't really have a direct answer. The Kerr black hole metric is an axially-symmetric solution of the Einstein field equation with a given mass and angular momentum, assuming that the spacetime is empty wherever the metric is well-defined.
I'll start with the Kerr metric in Kerr-Schild coordinates $t,x,y,z$, which is shown in equation (32) in "The Kerr spacetime: A brief introduction" (https://arxiv.org/abs/0706.0622). The equatorial plane is the plane defined by $t=z=0$. In this plane, the metric reduces to $$ ds^2=dx^2+dy^2+\frac{2m}{r}\left( \frac{r}{a^2+r^2}(x\,dx+y\,dy) + \frac{a}{a^2+r^2}(y\,dx-x\,dy) \right)^2 \tag{A.1} $$ where $s$ is the proper distance and where the function $r(x,y)$ is defined by $$ r^2 = x^2+y^2-a^2. \tag{A.2} $$ If we define new coordinates $\rho,\phi$ by $$ x=\rho\cos\phi \hskip2cm y = \rho\sin\phi, \tag{A.3} $$ then the metric (A.1) becomes $$ ds^2=d\rho^2+\rho^2 d\phi^2+\frac{2m}{r}\left( \frac{r}{\rho}\,d\rho + a\,d\phi \right)^2 \tag{A.4} $$ and the function $r$ is now given by $$ r^2 = \rho^2-a^2. $$ A circle centered on the symmetry axis has $d\rho=0$, so the proper distance along such a circle is given by $$ ds^2 =\left(\rho^2+\frac{2ma^2}{r}\right)d\phi^2 =\left(a^2+r^2+\frac{2ma^2}{r}\right)d\phi^2. \tag{A.5} $$ For a circle with given value of $\rho$, the proper circumference $K$ is calculated by integrating the proper distance $s$ over the range $0\leq\phi<2\pi$, which gives $$ K = 2\pi\sqrt{a^2+r^2+\frac{2ma^2}{r}}. \tag{A.6} $$ The minimum value of $K$ corresponds to the value of $r$ that satisfies $$ \frac{d}{dr}\left(r^2+\frac{2ma^2}{r}\right)=0, \tag{A.7} $$ namely $r=(ma^2)^{1/3}$. Using this in (A.6) gives the expression (3) for the minimum circumference.
The Kerr black hole has two event horizons, an outer horizon and an inner horizon, corresponding to these two values of $r$: $$ r_\pm =m\pm\sqrt{m^2-a^2}. \tag{A.8} $$ These satisfy $$ r_+ r_-=a^2 \tag{A.9} $$ which implies $$ \frac{r_+}{a}=\frac{a}{r_-}. \tag{A.10)} $$ This relationship together with the identity $$ a^2+r_\pm^2 = 2mr_\pm \tag{A.11} $$ can be used in (A.6) to show that the corresponding circumferences are both given by equation (1). In particular, the inner and outer event horizons have the same proper circumference in the equatorial plane. The circle with the minimum circumference (3) is sandwiched between these two event horizons.
The metric circumference in natural units of GM/c² is
$$ 2 \pi \sqrt{|g_{\phi \phi}|} = 2 \pi \sqrt{| \rm \frac{a^2 \sin ^4 \theta \left(a^2+r^2-2 r+\mho ^2\right)-\left(a^2+r^2\right)^2 \sin ^2 \theta }{a^2 \cos ^2 \theta+r^2}|} $$
where a=Jc/G/M² is the dimensionless spin parameter, and ℧=Q/M·√(K/G), so in the equatorial plane at θ=π/2 we get
$$ 2 \pi \sqrt{|g_{\phi \phi}|} = 2 \pi \sqrt{| \rm \frac{\left(a^2+r^2\right)^2-a^2 \left(a^2+r^2-2 r+\mho ^2\right)}{r^2}|}$$
which is infinity in the limit when r goes to 0 (the Boyer Lindquist coordinate radius of the singularity). The cartesian radius is
$$ \rm R = \sqrt{\Sigma} = \sqrt{r^2+a^2 \cos^2 \theta}$$
which is exactly aGM/c² on the equatorial plane, for a surface plot see here.
