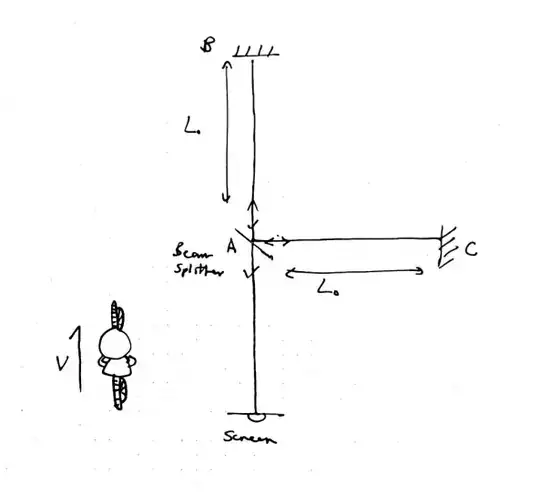
Say I am cycling past a Michelson interferometer set up. Someone at rest with the experiment will see both beams travelling a distance $L_0$ and hence conclude that $T_{AB}=T_{AC}=\frac{2L_0}{c}$.
However, according to me, the beam AB will not be travelling $L_0$, but a contracted distance $\frac{L_0}{\gamma}$, hence $T_{AB}=\frac{2L_0}{\gamma c}$. As AC is perpendicular to me and hence there is no relative motion along that axis, I don't observe AC to have any length contraction. However, I do still observe the whole light clock effect or time dilation. According to the observer at rest with the set up, the light beam travels along a horizontal line. According to me however, it travels diagonally, and the overall path $ACA$ describes a triangle. Hence, I see that $T_{AC}=\frac{2L_0 \gamma}{c}$.
This seems to imply I will observe interference while the observer at rest with the set up will not.
Note: $T_{AB}$ and $T_{AC}$ describe the time taken to travel the overall paths $ABA$ and $ACA$ respectively.