As the majority of concepts in dynamical systems are based on Manifolds. How can one think/imagine about the concept of a manifolds intuitively? (A Lucid explanation is highly encouraged!!!)
2 Answers
Someone asking about the intuition behind manifolds in dynamical systems is probably familiar with their definitions already, but for the sake of completeness, here it goes. For simplicity let's consider a fixed point $\mathbf{x}$ of a given dynamical system:
- Manifold: a set that looks Euclidean if you zoom in enough, i.e., it locally resembles $\mathbb{R}^n$;
- Stable manifold: the set of initial values that converge to $\mathbf{x}$ under the system dynamics;
- Unstable manifold: the set of initial values that converge to $\mathbf{x}$ under the inverse system dynamics.
These sets are interesting on their on, but they're often also central in the description of a system, in that the stable manifolds might act as boundaries, separating regions with qualitatively different behavior (e.g., converging to $0$ and diverging); while unstable manifolds can drive long-term behavior. For that reason they've been called a dynamical system skeleton.
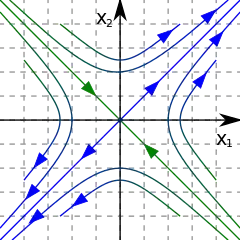
Let's consider a $2$D dynamical system and a fixed point $\mathbf{x}$ of it. The behavior in the immediate neighborhood of $\mathbf{x}$ is given by the linearization of the system equations around this point - let's say $\mathbf{x}$ is a saddle point, i.e., it has stable and unstable directions (straight lines in green and blue, respectively, in the figure below):
The green straight line is a boundary between two types of trajectories: those running to the top right and those running to the bottom left - which are the directions pointed by the (blue) unstable manifold arms.
If the system is linear, then these straight lines are already the stable and unstable manifolds of the fixed point, i.e.: any point on the green line converges asymptotically to the fixed point under the system dynamics, as do the points on the blue line, under its inverse dynamics. And most trajectories on the plane eventually diverge to either $+\infty$ or $-\infty$.
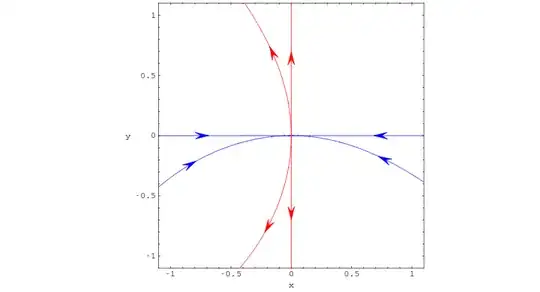
If the system is nonlinear, then typically the manifolds will coincide with these straight lines only on the point itself, smoothly curving away away from it, like displayed in this picture (source):
And, even further away from the fixed point, the manifolds might loose any relation to those straight lines, as for a damped pendulum:
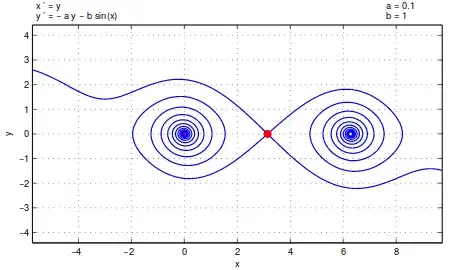
(Source.)
If you're learning Dynamical Systems, though, it's highly recommended to go through a textbook. A few suggestions can be found in Self-study book for dynamical systems theory?.
See, for instance, the explanation found in Alligood, Sauer, and Yorke's Chaos. An Introduction to Dynamical Systems (e-print):
- 13,064
First there's topology, a nice phrase I heard before was:"Topology was the geometry without numbers."
Second, there's geometry of space, which described by manifold as a quantitative representation as coordinates.
Third, in conservative fields in the manifold, there's potential conservation, uniqueness theorem and trajectories and orbits e.t.c.
Basically, you may consider draw a 2d grid on a piece of paper, then you what draw as pictures on the paper (flowers, squares, e.t.c.) was geometry. However, when you twist the paper, the grids in 3D perspective changes, the change of the grid was change of manifold. Think how pictures were changed when you manifold (geometry of paper/geometry of space, or say the grid of the paper) changed in the space.
- 1,076