Can someone shed some light on the following problem? I'm unable to get any traction on it as I know nothing about fluid dynamics (I'm a computer engineer).
It's a problem I made up over a lunch discussion with a friend. I've illustrated it as folows:
The pressure drop across a pipe, can be determined by means of the Fanning friction factor, $f$. For cylindrical pipes, the pressure drop is
$$\Delta p = 4f \frac{L}{D} \frac{1}{2}\rho v^2 $$
With $L$ the length of the pipe, $D$ the diameter (or hydraulic diameter for non-circular cross-sections), $\rho$ the density, and $v$ the mean velocity.
The friction factor is empirically determined, but for turbulent flow, you can use Blasius formula
$$4f = 0.316 Re^{-\frac{1}{4}}$$
where $Re$ is the Reynolds number of the flow ($=\frac{\rho v D}{\mu}$).
What the next step is, is to add the contributions by the three sections. You should realize that the average velocity in the different pipes is related via the flow rate. You will be able to solve this equation for $v$, and see the effect $r_2/r_1$ has.
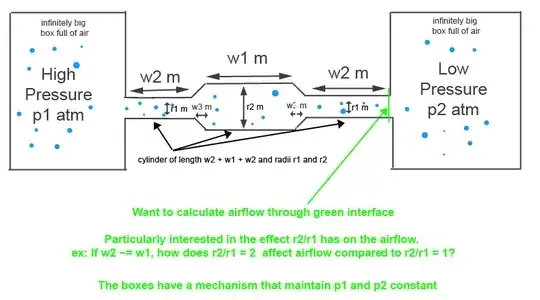
First we start with the incompressible Euler equations (so we will assume inviscid, more on this later):
$$\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j} = -\frac{1}{\rho}\frac{\partial P}{\partial x_i}$$
Because your chambers can maintain pressure forever, we are looking at a steady state solution so the time derivative goes away. And we can further assume that variations in the transverse directions are small in comparison to variations in the axial direction (more on this later too). This leaves us with:
$$u\frac{d u}{d x} = -\frac{1}{\rho}\frac{d P}{d x}$$
which you can solve directly to find the velocity at the end of the pipe before it opens into the second chamber. To do this, simply integrate from $x = 0$ which is defined as the start of the pipes connecting the two chambers to $x = 2w_2+w_1$ and $u = 0$ at $x = 0$.
When you do this, you'll find that the expansion in the middle has no effect on the flow at the end of the pipe. This is of course just Bernoulli's Principle (where you expand then contract again and end up right where you were before).
So how did we get here?
Well, first we assumed inviscid flow. See Bernhard's answer for how to account for that, but it is a very complicated problem in general and we typically have to rely on empirical relations (like those given). Ultimately you will end up with more losses which means less work can be done by the flow at the end.
Second, we assumed that variations in transverse directions were small in comparison to variations in the axial direction. By doing this, we implicitly require that $w_3$ is large enough that the area change is slow and the flow does not separate. If this is not the case and the flow does separate, then turbulence will be generated and the flow in the last section of pipe could be very turbulent. The contraction will serve to dampen the turbulence some due to the vortex stretching term of the vorticity equation. So if $w_3$ is small such that there is a rapid change in area, then the downstream flow will be turbulent and slower.
Third, we started with the incompressible form of the Euler equations. This requires that $P_1$ not be significantly bigger than $P_2$ so that the flow remains subsonic throughout. Let's look at what would happen if this were not the case and sonic flow was encountered.
Depending on how big the pressure difference is, sonic or supersonic flow could occur in a few different places. The first place it would go sonic is at the area contraction before the second small pipe. At that point, you have actually designed a blowdown wind tunnel where your throat is at the area contraction. It would be possible for the flow to continue accelerating to supersonic speeds without a shock forming if all the conditions were just right.
However, it's far more likely that a normal shock would form at the contraction. This shock would heat the air and bring the velocity back down to subsonic speeds.
If it were supersonic in the first section, then it would accelerate even more in the second section and then decelerate entering the third. This is virtually identical to the setup of the blowdown wind tunnel mentioned previously.
The pressure gradient will be used both to accelerate your fluid, as to overcome loses in the pipe system. Loses are normally divided into "major loses" which account for friction against the pipe walls, normally calculated with the Darcy-Weisbach equation, and "minor loses" which account for turbulent behavior in bends, valves, inlets, outlets and expansionas and contractions of the pipe. Here you have a pretty detailed explanation of where do some of those loses come from, and how to quantify them. In short, having that intermediate chamber will mean higher loses, and thus a lower airflow.
