The Four-Clock Special Relativity Conundrum

Question

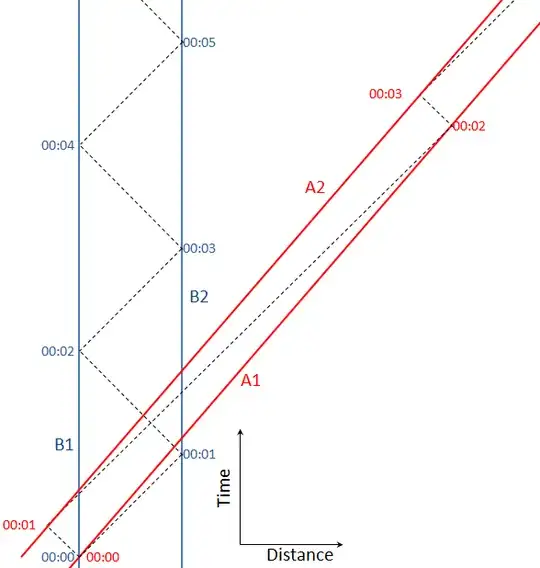
Two open-car trains approach each other at fixed velocities. Each has a radar to see how quickly the other train is approaching, but apart from that the trains have no a priori knowledge of each other.

Each train has engineers on its first and last cars. Each engineer has an atomic clock and a laser for communicating with their partner on the same train. Long before the trains meet, the engineers on each train use their lasers to adjust their relative separations to exactly one kilometer. Using the synchronization procedure first defined by Einstein, the engineers also exchange time data and use it to adjust their atomic clocks until they are precisely synchronized within their shared frame.

The trains meet. The clocks are positioned so that they almost touch as they pass. At the moment of nearest contact, they exchange and record each other's values (timestamps).

Some time later, the clocks on the trailing cars meet and perform the same procedure.

The delay between the leading and trailing data events can now be measured in two ways.

If the two timestamps taken from the first train are compared, the result is the time between the events as measured from the first train. This value is meaningful because the engineers on that train previously synchronized their clocks and stayed within the same frame of reference at all times. If the timestamps from the second train are used, a similar but distinct measurement of the time between the two events can be obtained.

Now, three questions:

1. Is there anything wrong or impossible with this experimental setup? If so, what is it?

2. If you accept the experiment as realistic and meaningful, will the delays calculated from the perspective of each of the two trains be the same, or different?

3. If you answered "different," what is the correct procedure for predicting in advance what the ratio of the two delays will be?

---

2013-01-10 - The Answer(s!)

I awarded the bounty to @FrankH for pages of excellent and educational work worth of reading by anyone who wants to understand special relativity better.

However, I've also taken the unusual step of re-allocating the answer designation to @MatthewMcIrvin.

There are two reasons: (1) Matthew McIrvin was the first one to spot the importance of the symmetric-velocities frame, which others ended up gravitating (heh!) to; and (2) Matthew's answer is short, which is great for readers in a hurry. FrankH, sorry about the switch, but I didn't realize I could split them before.

So: If you are not overly familiar with special relativity and want to understand the full range of issues, I definitely recommend FrankH's answer. But if you already know SR pretty well and want the key insights quickly, please look at Matthew McIrvin's answer.

I will have more "proximate data exchange" SR questions sometime in the near future. Two frames turns out to be a very special case, but I had to start somewhere.

---

For folks with strong minds, stout hearts, and plenty of time to kill, a much more precise version of the above question is provided below. It requires new notations, alas.

To reduce the growing size of this question, I have deleted all earlier versions of it. You can still find them in the change history.

---

Precise version of the 4-clock conundrum

Please see the first three figures below. They define two new operators, the frame view and clock synchronization operators, that make the problem easier to state precisely:

---

---

---

---

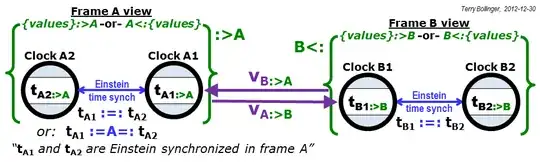
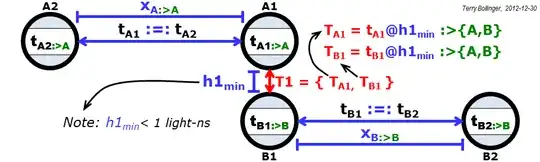
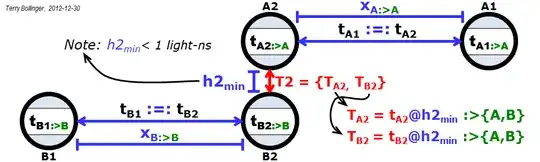
Note that the four timestamps $\{T_{A1}, T_{B1}, T_{A2}, T_{B2}\}:>\{A,B\}$. That is, the four timestamps are shared and agreed to (with an accuracy of about 1 nanosecond in this case) by observers from both of the interacting frames A or B. Since T1 and T2 are historically recorded local events, this assertion can be further generalized to $\{T1,T2\}:>*$, where $*$ represents all possible frames. (And yes, $:>$ is two eyes looking left, while $<:$ is two eyes looking to the right.)

Using the four shared time stamps, define:

$T_{\Delta{A}} = T_{A2} - T_{A1}$

$T_{\Delta{B}} = T_{B2} - T_{B1}$

My main question is this:

---

Assuming that $T_{\Delta{A}} = f(T_{\Delta{B}})$ exists, what is $f(x)$?

---

Analysis (why this problem is difficult)

Based purely on symmetry in the setup, the most obvious answer is $f(x)=x$, that is:

$T_{\Delta{A}} = T_{\Delta{B}}$

There are some interesting reasons to be troubled by that seemingly straightforward and even obvious conclusion, not the least of which is that it violates the whole concept of special relativity (the Dingle heresy).

That is, if you assume $f(x)=x$ and follow that line of logic through to its logical conclusion, you quickly end up with time that flows the same for all frames -- that is, no relativity. Such a conclusion is in flat violation of over a century of very detailed experimental evidence, and so is just not supportable.

The following four figures show why it's so hard to assert that $T_{\Delta{A}} = T_{\Delta{B}}$ without violating special relativity.

---

---

---

---

---

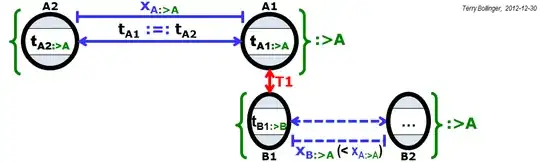
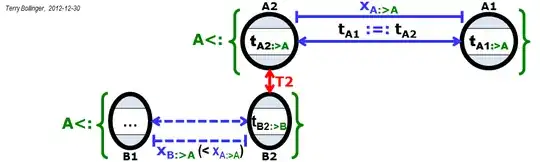
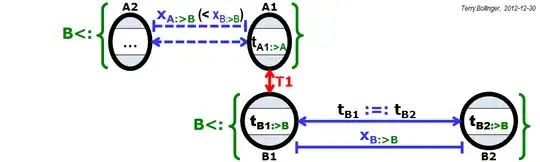
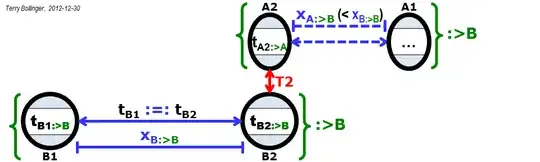
While the above figures accurately capture the reality of relativistic contraction of both distance and time, the problem in this case is simple: How do you decide which frame to select? The experiment as described can only give one outcome. Which one will it be?

Answer 1

The problem is that although A1 and A2 think the A clocks are perfectly synchronized and that B1 and B2 think that the B clocks are perfectly synchronized, neither pair will agree that the other pairs clocks are synchronized at all. This is the relativity of simultaneity of Special Relativity. *In particular the diagram in the original question (that diagram has now been removed) where all four clocks are showing 00:00 is wrong - no observer will agree that all four clocks are synchronized like that.*

It is almost always confusing to think about the time dilation and length contraction. It is always clearer and less ambiguous to draw a space-time diagram of the situation. In the following picture that is drawn in the B1/B2 rest frame I drew all the B world lines and clock readings in blue, all the A world lines and clock readings are in red and light signals are in black dashed lines. This is for a relative speed of approximately 0.866c between the rest frames to the best of my humble drawing abilities:

When B1 and A1 were at the same location (to within a foot) their clocks both said 00:00. The dotted lines are the light signals that always travel at speed "c" for all observers. The speed "c" is assumed to be drawn by lines at 45 degrees in this diagram. You can see that from the B1/B2 rest frame point of view, the A2 clock turns to 00:01 shortly after both A1 & B1 clocks turn to 00:00. However from the B1/B2 point of view, it takes a long time for A2's clock to turn to 00:02. That is why B1/B2 thinks that the A1/A2 clocks are not synchronized - it's because A1 is running away from the light signal while A2 is running towards the light signal.

From the diagram you can also see that B1 thinks A1's clock is running at half speed since when B1's clock reads 00:04, he predicts that A1's clock will read 00:02 in B1's rest frame based on the timing of the light signals that A1 and A2 are passing back and forth. However, B1 will NOT think that A1 and A2's clocks are synchronized - A2 clicks over to the next second significantly sooner than A1's clock goes to the next second. Also to B1 and B2 it looks like A1 and A2 are a lot closer together than 1 light second - in particular A1 and A2 are about a half light second apart as measured by B's clocks.

There are 4 events where a red line crosses a blue line. The experimental results are the values of the two clocks that are crossing each other. Here are the approximate results as read out from the imperfectly drawn diagram and after interpolating the clock readings:

• A1 meets B1: A1=00:00.0, B1=00:00.0
• A2 meets B1: A2~00:01.2, B1~00:00.8
• A1 meets B2: A1~00:00.8, B2~00:01.2
• A2 meets B2: A1~00:01.7, B2~00:01.7

The counter intuitive thing about Special Relativity is that if you just swap all the A and B labels, you would get exactly the same figure from the point of view of A1 and A2's rest frame. So A1 and A2 will think that B's clocks are not synchronized and that B's clocks are running slow and that B1 and B2 are a half light second apart.

From this A <=> B switched diagram which is the A1/A2 rest frame, we would then get the following experimental results:

• B1 meets A1: B1=00:00.0, A1=00:00.0
• B2 meets A1: B2~00:01.2, A1~00:00.8
• B1 meets A2: B1~00:00.8, A2~00:01.2
• B2 meets A2: B1~00:01.7, A2~00:01.7

This is the same results as in the B1/B2 rest frame diagram.

Note that in both of these lists of four events, the 1st and 4th events are at timelike separations so all observers will agree on the order of these events. However, the 2nd and 3rd events on both lists are at spacelike separations so different observers will disagree about the ordering of those events. In fact there are observers where these events would be seen as simultaneous. However, for all observers the values shown on the clocks that are passing each other at all four events will be the same consistent sets of values shown in these lists.

That is about all there is to it. This is the theoretically predicted outcome of the experiment.

Update on 1/4/2012 for the updated question:

Reading from the values shown above and using the new notation of the question:

$T_{A1} = 0, T_{B1} = 0, T_{A2} = 1.7, T_{B2} = 1.7, $

and therefore:

$T_{\Delta A} = T_{\Delta B} $

Basically, in a given observers rest frame, he thinks his clock went from 0 to 1.7 but he thinks the other guys trailing clock went from 0.85 to 1.7 so it is running at half speed. The 0.85 comes from the relativity of simultaneity of special relativity. In the observers rest frame he will admit that the first of the other clocks started at 0 but that the second of the other clocks was already at 0.85 at that point and thus the other guys clocks are not synchronized.

Answer 2

By symmetry, the rear clocks read the same time as each other when they pass.

This is possible because simultaneity is relative. For example, from frame A, the rear clock B is running slowly, but was also ahead of the front clock (even though the B clocks are synchronous in their own frame). Running slowly but with a head start, the clocks sync up when they cross.

By the way, your graphics make incorrect assumptions. First, you show the clocks being synchronized in a "neutral" frame where they all have the same speed. Next, you show clocks A still synchronized in their rest frame. This isn't correct; they can only be synchronized in one of these frames. See http://en.wikipedia.org/wiki/Relativity_of_simultaneity

Here is a full blow-by-blow. The event A1 = B1 be the mutual origin for all three reference frames. Let clocks A1 and B1 read zero at that event. Let the distance from A1 to A2 be 1 in its own frame, and likewise for B. Let the velocity of B in frame A be -0.866 so that $\gamma = 2$.

We'll find the coordinates of all the clocks in all the frames. (x,t) denotes the space and time coordinates in that frame. "tA1: 0" means that the time read on clock A1 is zero. The procedure is that we first find the coordinates in the frame we're working on. Then, if we want to know what a clock reads, that's equivalent to ask what the time coordinate of that event is in its own frame, so we Lorentz-transform into the clock's own frame to find what time it reads.

Frame A In this frame, clocks A1 and A2 are stationary. B1 and B2 are moving at -0.866 and are separated by a distance 1/2 because of lorentz contraction.

Event A1 = B1 and simultaneously with it

A1 = (0,0)

B1 = (0,0)

A2 = (-1,0)

B2 = (1/2,0)

tA1 = 0

tB1 = 0

tA2 = 0 (synchronized with A1 in this frame)

tB2 = 0.866 (by Lorentz-transforming its coordinates)

Event A2 = B2

A1 = (0, 1.732) (the time comes from the distance B2 had to move, 3/2, divided by its speed, 0.866)

B1 = (-1.5, 1.732) (travels the same 3/2 distance as B2)

A2 = (-1, 1.732) (same time as A1 by synchronization)

B2 = (-1, 1.732) (same event at A2)

tA1 = 1.732

tB1 = .866 (by Lorentz-transforming its coordinates)

tA2 = 1.732

tB2 = 1.732 (by Lorentz-transforming its coordinates)

As you can see, in this frame, B's clocks are both running slowly. However, B's clocks are not synchronized to each other in this frame. They are synchronized only in their own frame. In this frame, clock B2 runs ahead of clock B1. Since it's ahead but running slowly, it reads exactly the same times as A2 when they pass each other.

Frame B In this frame clocks B1 and B2 are stationary. A1 and A2 are moving at 0.866 and are separated by a distance 1/2 because of lorentz contraction.

Event A1 = B1 and simultaneously with it

A1 = (0,0)

B1 = (0,0)

A2 = (-1/2,0)

B2 = (1,0)

tA1 = 0

tB1 = 0

tA2 = 0.866 (by Lorentz-transforming its coordinates)

tB2 = 0 (synchronized with B1 in this frame)

Event A2 = B2

A1 = (1.5, 1.732)

B1 = (0, 1.732)

A2 = (-1, 1.732)

B2 = (-1, 1.732)

tA1 = .866

tB1 = 1.732

tA2 = 1.732

tB2 = 1.732

This frame is the same as frame A, but with the labels switched. Again, the clocks A, which were synchronized in their own frame, are not synchronized here. When we Lorentz-transform all the coordinates involved, we find that time dilation works exactly as expected.

Frame C This is the neutral frame where each pair of clock is coming in from the side. Their velocities work out to $\pm 0.577$ and $\gamma = 1.23$

Event A1 = B1

A1 = (0,0)

B1 = (0,0)

A2 = (-.816,0)

B2 = (.816,0)

tA1 = 0

tB1 = 0

tA2 = .577 (by Lorentz-transforming its coordinates to frame A)

tB2 = .577 (by Lorentz-transforming its coordinates to frame B)

Event A2 = B2

A1 = (.816, 1.41) (x comes from A1-A2 distance. Time comes from distance moved/velocity)

B1 = (-.816, 1.41)

A2 = (0, 1.41)

B2 = (0, 1.41)

tA1 = 1.15

tB1 = 1.15

tA2 = 1.73

tB2 = 1.73 (all found by Lorentz-transforming into the clock's frame)

As we can see, all the clocks show the appropriate time dilation in this frame. In this frame, clocks A1 and B1 always show the same time, but run slowly. A2 and B2 similarly show the same time, run slowly by the same amount, but lag the other two by a constant amount.

Answer 3

I'm not sure, but I think your objection here is that the times measured by these observers for the interval between the "A1 meets B1" and "A2 meets B2" events is the same, even though they're in frames that are moving relative to one another. So shouldn't there be some kind of time dilation?

This is not a problem, though. The familiar relativistic time dilation formula has to do with the time t' you'll measure between two events, relative to the time t between the events in the frame where they occur at the same location--that is, their rest frame, the frame in which a single stationary clock could mark time for the two events. t'/t = gamma, the time dilation factor.

What is the rest frame defined by these two events? It's not the frame moving with either train. It's a third frame: the frame in which the two trains are moving in opposite directions with the same speed! (Call it the "center of velocity" frame.) In this frame, A1 passes B1 and A2 passes B2 at exactly the same place.

Relative to this center-of-velocity frame, both train frames are moving at the same speed, just in opposite directions.

So the elapsed time between the two events gets time-dilated to exactly the same extent to observers on the two trains. The measured time won't be the same in every frame; but it will be the same in those two particular frames!

Answer 4

The Boost along x Lorentz transformation is ideally suited for settling the conundrum quickly and easily. For an event recorded at (x,t) in the lab, the boosted frame will record a $t'$ for the same event as $$ t' =\gamma(t - vx/c^2)$$

We use this to find the time shown on $A2$ and $B2$ at the instant $A1$ and $B1$ pass one another at t=0: $$t'_{A2} =\gamma(0 - vx/c^2)\quad t''_{B2} =\gamma(0 - vx/c^2) $$

They therefore show the same time, and will continue to do so since they're travelling at the same speed.

Answer 5

Is there anything wrong or impossible with this experimental setup? If so, what is it?

I don't see any issues with your setup.

If you accept the experiment as realistic and meaningful, will the delays calculated from the perspective of each of the two trains be the same, or different?

(Yet again) the 2 delays are the same.

I. kinematic analysis:

• Both trains have length $L$ (measured in the rest frame of the train under consideration).
• In A's reference frame, B approaches at speed $v$ and has length $L/\gamma$, with $\gamma = 1/\sqrt{1-(v/c)^2}$.
• If A1 meets B1 at time 0, A1 meets B2 at time $L/(\gamma v)$, A2 meeets B1 at time $L/v$, and A2 meets B2 at time $T_{\Delta A}=(L/v)(1+1/\gamma)$.
• In B's reference frame, the analysis is identical, giving the same result.

II. Alternatively, considered as space-time events (addressing your comment to Spacelike Cadet (love that name!)), it is certainly true that there is an invariant interval $ds$ between the passings of the leading and of the ending cars.

• In A's reference frame, that interval is $ds^2 = (cT_{\Delta A})^2 - L^2$.
• In B's reference frame, that interval is $ds^2 = (cT_{\Delta B})^2 - L^2$.

The crucial point is that both trains have "rest length" $L$, so it follows immediately that $T_{\Delta A}=T_{\Delta B}$. The time-like separations are the same only because the train lengths are identical.

• The invariant interval is $ds= \frac{L}{v} \sqrt{\frac{2}{\gamma} + \frac{2}{\gamma^2}}$.

If you answered "different," what is the correct procedure for predicting in advance what the ratio of the two delays will be?

N/A.

---

Update: As a check, here's an analysis in the "Center of Velocity" (aka CV) frame.

• In the CV frame, both trains approach with velocity $\pm v_{CV}$ $$ v_{CV} = \frac{v}{1+\sqrt{1-(v/c)^2}} = \frac{v}{1+\frac{1}{\gamma}}$$ (Note it's not just $v/2$! You can check this result by applying the addition-of-velocities formula to $v_{CV}$ and the relative train velocity $-v$, with the result being just $-v_{CV}$, the equal-and-opposite velocity of the other train in the CV frame.)
• In the CV frame, both the first and last car crossings occur at the origin, and both trains are Lorentz-contracted to length $L/\gamma_{CV}$ with $\gamma_{CV}=1/\sqrt{1-(v_{CV}/c)^2}$.
• The time duration between first and last car crossings is then $$ T_{\Delta CV} = \frac{L}{\gamma_{CV}} \frac{1}{v_{CV}} $$ Plugging and chugging through the algebra, one finds: $$ T_{\Delta CV} = \frac{L}{v} \sqrt{\frac{2}{\gamma}+\frac{2}{\gamma^2}} $$ This result is different from $T_{\Delta A}=T_{\Delta B}$.
• The invariant interval between the two end-crossing events in the CV frame is just: $$ ds^2 = (c T_{\Delta CV})^2 $$ since both crossings happen at the CV origin, and $ds$ works out to be exactly the same as calculated in the A and B frames (as it must).

Answer 6

What follows here is an answer entirely uninfluenced by other answers. I have created it entirely from the initial problem statement.

Let there be four worldlines: $A_f$ for the front of the first train, $A_r$ for the rear of the first train. $B_f$ for the front of the second train, $B_r$ for the rear of the second train.

These worldlines can be parameterized as follows.

$$\begin{align*} A_f(\tau) &= u_A \tau \\ B_f(\tau) &= u_B \tau \end{align*}$$

$u_A$ and $u_B$ are four-velocities. Here, we assume that at $\tau = 0$, the fronts of the two trains are coincident at the origin.

What we want to do now is figure out where the proper locations for the rears of the train should be. Without loss of generality, we can set these locations to be some distance $d$. We can, through an orthonormalization procedure, find the spacelike vectors that go along the trains' lengths. My background is in the clifford spacetime algebra, where we would represent this quantity as $iu$. Hence, the other two worldlines are:

$$\begin{align*} A_r(\tau) &= (\tau - di) u_A \\ B_r(\tau) &= (\tau + di) u_B \end{align*}$$

Choosing minus for the A train ensures that the rear of the train is further down the -x-axis than the front. It should be noted that then the $A_r, A_f$ worldlines are described by $\tau$, the proper time of the A train. Similarly for the B worldlines; these proper times are different between the trains, of course.

Now, we should be able to compute the intersection by saying $A_r(\tau_A) = B_r(\tau_B)$ for two different proper time intervals $\tau_A, \tau_B$. There are two vector components, so the system is well-described.

Now, for simplicity, we choose $u_A = e_t$, the time basis vector. Thus, we choose a frame where the A train stays still and B moves past, from right to left. $u_B = \gamma(e_t - \beta e_x)$ then, and $i u_B = \gamma(e_x - \beta e_t)$. The equations look like

$$\begin{align*}\tau_A &= \gamma \tau_B - \gamma \beta d \\ - d &= -\gamma \beta \tau_B + \gamma d \end{align*}$$

These equations are easily solved. At first glance, the solution appears to be

$$\begin{align*} \tau_B &= \frac{(\gamma + 1) d}{\gamma \beta} \\ \tau_A &= \frac{(\gamma + 1) d}{\beta} - \gamma \beta d \end{align*}$$

But a little mathematical manipulation (in particular, using $\gamma = (1-\beta^2)^{-1/2}$), proves them to be the same.

$$\begin{align*} \tau_A &= \frac{d(1+\gamma) - \beta^2 d \gamma}{\beta} \\ &= \frac{d(1 + \gamma[1-\beta^2])}{\beta} \\ &= \frac{d(1+1/\gamma)}{\beta}\\ &= \frac{d(\gamma + 1)}{\gamma \beta}\end{align*}$$

In short, then,

1) There is nothing wrong with the experimental setup.

2) As expected by symmetry of the problem (each train should measure the relative velocity of the other to be the same), the time delays measured by each train are the same, and they can be calculated according to the above calculation.

Answer 7

The effort you are putting in to this question is admirable. You most certainly deserve a satisfactory answer.

Your question is: as a matter of principle Special Relativity asserts total symmetry: how is that accommodated?

The diagrams that you are creating are at best snapshots of the ongoing process. I believe you need to create an animation. I believe you need to create an animation to explain it to yourself. I say that because I did that too: I created an animation. The process of working out how things proceed over time, so that the animation was correct, helped me absorb the most counter-intuitive aspects of SR.

Let me recount a memory. As a teenager I would read books for kids about science/physics. I would read about special relativity too, I looked at the diagrams, and I was aware that I didn't understand it, at least not to my satisfaction. At some point there was a series of educational television programs about relativity. With the usual trains. But being television the creators of that series had taken the opportunity to present the spacetime physics with an animation!

I remember it vividly: Einstein on one train and Poincaré on the other, clocks in the front, the middle, and the rear, the trains passing each other. Most importantly: the shift of reference frame from one train to the other was also represented in animated form! At the start you had the spatial axis (horizontal) and the time axis (vertical) at right angles to each other. When that coordinate system is subjected to a Lorentz transformation the axes move relative to each other in a scissor-like manner. And I saw the complete symmetry. You can use a frame co-moving with the Einstein train or a frame co-moving with the Poincaré train, and you can transform symmetrically between them.

Years later I wanted to experience that vividness again, and I created an animation like the animation in that television program I remembered. The animation I created depicts pulses of light shuttling between clocks, etc., etc. (Incidentally; that animation isn't just lying around, I added it to my website.)

Answer 8

The answer, as others have said, is that they mark the same time delay. So the task is to give an explanation that addresses the root of the confusion.

I think it comes down to this: at the four events where two moving observers meet, both observers directly observe that the other clock is moving more slowly, right? Well, except time dilation is not a direct observation.

Put it this way: on the one hand you seem to be trying to consider signals sent and received, and coincident (or nearly coincident) events, like the (near) meeting of observers. But the principle that moving clocks run slow has no direct meaning in those terms, it is understood in terms of simultaneous spaces. In terms of signals sent and received, the principle is that oncoming clocks run fast and outgoing clocks run slow.

Maybe it will be instructive to look at this purely from the signal framework. In what follows, distances will be radar distances, and times will be reception times. That is, if you now receive the echo of a radar pulse that you sent some time $\Delta t$ ago, then we say that now, the distance to the object it bounced off of is $\frac{c}{2}\Delta t$. (Your point of view is what you see, your past light cone is now.) Formally, the metric is:

$$d\tau^2 = dt^2 - \frac{2}{c}dr\cdot dt - \frac{r^2}{c^2} d\Omega^2$$

from which certain relevant facts can be derived:

• The time expansion factor for a radially moving clock is: $$k = \sqrt{1 - \frac{2v}{c}}$$ $v$ is the velocity, the rate of change of (radar) distance with respect to (reception) time. For outgoing clocks, $v>0$, so $k<1$, they run slow. For incoming clocks, $v<0$, so $k>1$, they run fast. (In the extreme case, the speed of outgoing light is $\frac{c}{2}$, and the speed of oncoming light is infinite.)

• $k$ is also the length expansion factor (in the radial direction).

• When an oncoming objects meets and passes us, its expansion factor goes from $k$ to $k^{-1}$, and its velocity goes from $v$ to: $$v^\star = -\frac{cv}{c-2v}$$

For comparison, the "frame" velocity, the usual way of reckoning speeds, is $\frac{cv}{c-v}$. But this frame velocity is not directly observed.

We can now address the sequence of events from the point of view of the front (F) and back (B) of the train. The clocks at the front and back of the train are synchronised in the sense that they each see the other running at the same rate, but at a time $\epsilon$ behind. The distance between the two clocks is a constant, $\epsilon c$, which is the length of the train.

Let us say the oncoming train has speed $\frac{3}{2}c$, so that $k=2$. It is twice as long as ours, $2\epsilon c$. Its clocks (F',B') are running at twice the rate of ours.

Front:

• We meet F', say at time $T$, which we record. F' records its time, say, $T'$. Now F' is outgoing, and its speed becomes $\frac{3}{8}c$, and its clock starts running at half the rate of ours. Meanwhile B' is still oncoming at $\frac{3}{2}c$, its clock is showing $T' - \epsilon$ and still running at twice the rate of ours, and it is $2\epsilon c$ away.

• At $T + \frac{4}{3}\epsilon$, we meet B'. Its clock is showing $T' + \frac{5}{3}\epsilon$, and starts running at half our rate. In which time F' has travelled $\frac{1}{2}\epsilon c$, so the length of the other train has shrunk to half the length of ours. B' is now also outgoing at $\frac{3}{8}c$, so the other train stops shrinking. F' is still $\frac{1}{2}\epsilon c$ away from B, and its clock is showing $T' + \frac{2}{3}\epsilon$.

• At $T + \frac{8}{3}\epsilon$, F' meets B. B' shows $T' + \frac{7}{3}\epsilon$, while F' shows $T' + \frac{4}{3}\epsilon$.

• At $T + 4\epsilon$, B' meets B. The clock at B is $\epsilon$ behind ours, so it is showing $T + 3\epsilon$, which it records. B' is showing $T' + 3\epsilon$, which it records, while F' is showing $T' + 2\epsilon$.

Back:

• At $T + \epsilon$, F meets F'. F, whose clock is $\epsilon$ behind ours, records $T$. F' records $T'$. B' shows $T' - \epsilon$. Both F' and B' are still oncoming at $\frac{3}{2}c$, and their clocks are still running at double rate. F' is $\epsilon c$ away.

• At $T + \frac{5}{3}\epsilon$, we meet F'. The other train is still twice as long as ours, so B' is still $\epsilon c$ away from F, and $2\epsilon c$ away from us. F' shows $T' + \frac{4}{3}\epsilon$, and its clock starts running at half rate, while B' shows $T' + \frac{1}{3}\epsilon$ and is still running at double rate.

• At $T + \frac{7}{3}\epsilon$, F meets B'. F' shows $T' + \frac{5}{3}\epsilon$, and so does B'.

• At $T + 3\epsilon$, we meet B' and record our time. F' shows $T' + 2\epsilon$, while B' shows $T' + 3\epsilon$, which it records.

[Addendum]

I'll add the "neutral observer" O to this, as suggested by Dr. Matt McIrvin. O is the one who sees F meeting F' as happening in the same place as B meeting B'. From either train's perspective, O's expansion factor will $\sqrt{2}$ approaching and $\frac{1}{\sqrt{2}}$ receding -- in general, its expansion factor will be the square root.

So, O is oncoming at speed $v = -\frac{c}{2}$ and its clock is running $\sqrt{2}$ times fast.

Now from F's perspective, F meets both O and F' at time $T$, and O records time, say, $T_O$. O is now outgoing at speed $v = +\frac{c}{4}$ and its clock starts running $\sqrt{2}$ times slow. So B, which is $\epsilon c$ away, will meet O at $T + 4\epsilon$, which is also when it will meet B', and O will record time $T_O + 2\sqrt{2}\epsilon$.

From B's perspective, F meets both O and F' at time $T+\epsilon$. O is still oncmoing at speed $v = -\frac{c}{2}$ and its clock is still running $\sqrt{2}$ times fast. So O arrives at time $T + 3\epsilon$, which is also when B' arrives, and O records time $T_O + 2\sqrt{2}\epsilon$.

From O's perspective, either train is initially oncoming at speed $\frac{c}{2}$ and its clocks are running $\sqrt{2}$ times fast, and its length is $\sqrt{2}\epsilon c$. At time $T_O$ O meets F, which marks time $T$. Now F is outgoing at speed $\frac{c}{4}$ and its clock is running $\sqrt{2}$ times slow. Meanwhile B is still oncoming at $\frac{c}{2}$. Its clock shows $T - \epsilon$, and it is still running $\sqrt{2}$ times fast, and it is $\sqrt{2}\epsilon c$ away. So it arrives at time $T_O + 2\sqrt{2}\epsilon c$, at which point its clock shows $T + 3\epsilon$, which it records. Meanwhile F has travelled a distance $\frac{1}{\sqrt{2}}\epsilon c$, so the train has shrunk to that length. And O sees exactly the same thing for the other train in the other direction.

Answer 9

This is simply an illustration of the reciprocity of time dilation. If you measure the duration by comparing the readings of the two clocks on one train, you will get some answer T. If you measure the duration with the leading clock on either train you will get some other answer t, and t will be shorter than T in accordance with the usual time dilation formula.

The so-called Dingle heresy is a straightforward misunderstanding. In time dilation, you are not directly comparing the rate of a clock in one frame with a clock in another- you are comparing an elapsed time recorded by one clock with the readings on two other clocks it passes, so the issue of simultaneity is what is actually at the heart of it.