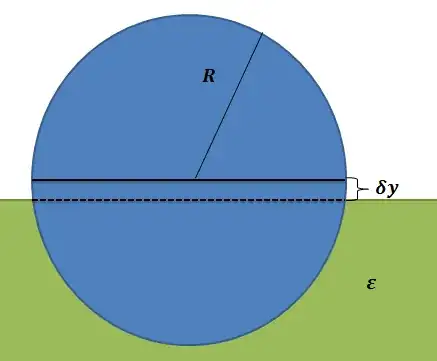
This is a classic problem in electrostatics with a twist, so I thought it could be useful for others here. I did have a problem with the integration at the end, but on general I think the idea can help others.
The idea is that a conductor, chargeless sphere of radius R is floating half-submerged on a liquid with dielectric constant (the upper half is in air, with dielectric constant equal 1). Now a differential of charge $\delta Q$ is added to the surface and the sphere moves, and we want to find how much it displaces.
Question
Find the displacement of the sphere in terms of the differential charge
My attempt at a solution
While I don't know if it's really useful, if we apply mechanical equilibrium before adding the charge, it's straightforward to find that $\rho_s=\rho_l$, where $\rho_s$ and $\rho_l$ are the volumetric densities of the sphere and the liquid, respectively.
After adding the charge, we can suppose that the sphere moves upwards (the direction doesn't matter, since at the end the sign will determine the correct one). Assuming the charge distributes uniformily over the surface, we can apply Gauss Law to find that:
$$\int_{air} \vec{D}\cdot d\vec{A}+\int_{liquid}\vec{D}\cdot d\vec{A}=\delta Q$$
Letting $\delta y$ be the vertical distance that the sphere moves up (the area is a small ring of perimeter $2\pi R$ and height $\delta y$), and since the electric field (and thus the displacement) of a submerged sphere is radial:
$$D_{air}(2\pi R^2+2\pi \delta y)+D_{liquid}(2\pi R^2-2\pi \delta y)=\delta Q$$
Assuming an isotropic, homogenous, linear dielectric, we can apply the constitutive relationship $\vec{D}=\epsilon \vec{E}$ to find that:
$$\vec{E}=\frac{1}{2\pi a}\frac{\delta Q}{(a+\delta y)+\epsilon(a-\delta y)}$$
And thus:
$$\vec{D_{air}}=\frac{1}{2\pi a}\frac{\delta Q}{(a+\delta y)+\epsilon(a-\delta y)}$$
$$\vec{D_{liquid}}=\frac{\epsilon}{2\pi a}\frac{\delta Q}{(a+\delta y)+\epsilon(a-\delta y)}$$
Now, for these kinds of materials, the energy of the fields is:
$$U_E=\int d^3 r \vec{E}\cdot\vec{D}$$
Substituting:
$$U_E=\frac{(\delta Q)^2}{4\pi^2 a^2}\left ( \int_{air} \frac{d^3r}{((a+\delta y)+\epsilon(a-\delta y))^2} + \epsilon\int_{liquid} \frac{d^3r}{((a+\delta y)+\epsilon(a-\delta y))^2} \right )$$
To first order, we can simplify the denominator since $\delta y$ is small:
$$((a+\delta y)+\epsilon(a-\delta y))^2=a^2(1+3\epsilon)+2a\delta y(1-\epsilon^2)$$
Therefore:
$$U_E=\frac{(\delta Q)^2}{4\pi^2 a^2}\left ( \int_{air} \frac{d^3r}{a^2(1+3\epsilon)+2a\delta y(1-\epsilon^2)} + \epsilon\int_{liquid} \frac{d^3r}{a^2(1+3\epsilon)+2a\delta y(1-\epsilon^2)} \right )$$
Now, if we could just express $\delta y$ as a function of spherical coordinates we could perform the integral, so I got stuck here.
However, assuming we can do the above integral, we can easily find the force as:
$$F_E=-\left ( \frac{\partial U_E}{\partial R} \right )_{\delta Q}$$
And perform a new mechanical equilibrium equation:
$$\rho_l V_{submerged} g - \rho_s V_{total} g +F_E=0$$
And theoretically find the submerged volume to find the percentage that the sphere moved after adding the charge (don't forget we calculated $\rho_s=\rho_l/2$)
If I'm allowed to ask: is my intuition about finding the displacement correct? Or how can I find it if I consider a virtual displacement aroound the equilibrium position instead?
I have received the suggestion to consider the equilibrium state and then apply a first order perturbation in $\delta Q$, which should be easier but I can't find a way to do it this way.