It's given that CA - CB is d, the angle CAE is $\theta$. (E is not on the normal of mirror M1). I want to find the condition for maxima at E (as a function of $\theta$).
I tried finding the path difference but it turned out to be very complicated, assuming that light after passing through beamsplitter continues traveling along the same straight line. How does one find the radius of rings formed on the screen, if there's a screen instead of detector?
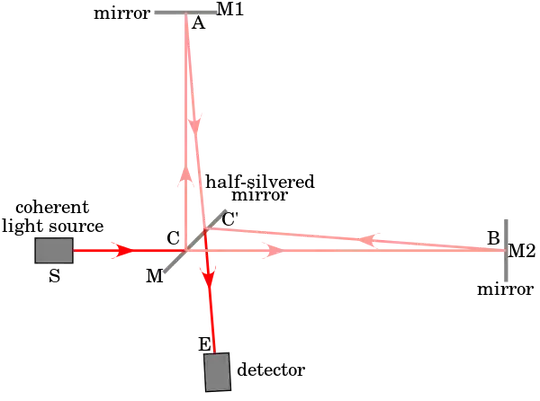
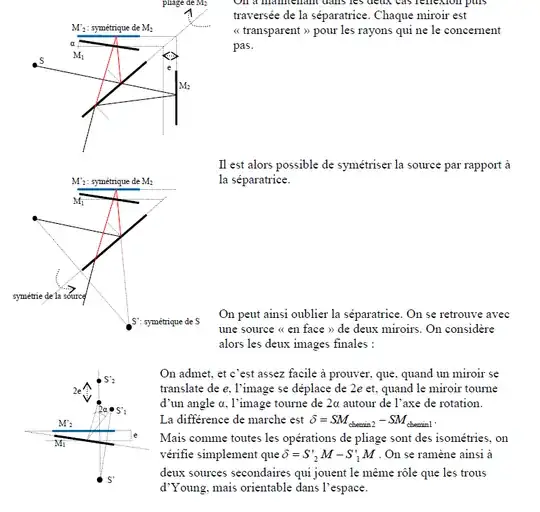
It is much easier to "fold" the interferometer. If you imagine that there is a lens of short focal length at the exit of the laser, (otherwise, the rays do not diverge), you have a point source S which after reflection on the separator and the mirrors has two images S1 and S2 at the top, distant from $2d$. (When you move a mirror by $d$, the image move by $2d$)
If the screen is at a sufficiently large distance, the rays emitted by S1 and S2 which interfere at E are practically parallel and the difference in the path is $\delta =2d\cos (\theta )$ (if there is no additional phase shift due to reflections on the mirrors ).
The bright rings correspond to $\delta =2d\cos ({{\theta }_{n}})=n\lambda $ and the rings on the screen are obtained by writing $\tan ({{\theta }_{n}})\approx {{\theta }_{n}}={{R}_{n}}/D$ if $D$ is the distance of the sources on the screen.
Be careful : the order of interference is maximum in the center and decreases when one moves away from the center.
