Applying energy and momentum conservation to the problem of pulling a bent carpet at a constant speed

Question

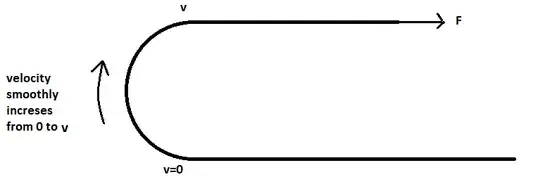
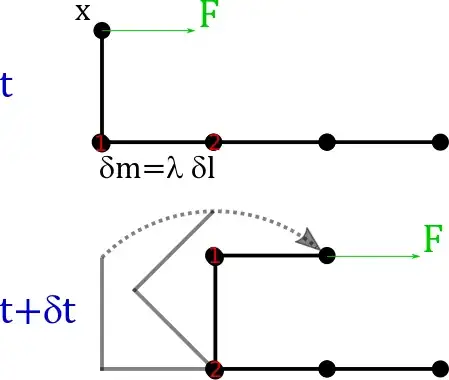
Consider this system.

A long, thin, pliable carpet is laid on a floor. One end of the carpet is bent back and then pulled backwards with constant speed $v$, just above the part of the carpet which is still at rest on the floor. What is the minimum force needed to pull the moving part if the carpet has mass $m$ per unit length?

Three different approaches lead to 2 different values for the minimal force: $\frac{mv^2}{4}$ and $\frac{mv^2}{2}$. Which ones are correct? How does energy and momentum conservation happen in this specific system?

I believe correct answer to this question might be useful for general audiences and for pedagogical reasons, because it addresses a certain mistake that people often do in similar problems.

My effort at answering the question. I get the answer $\color{blue}{F_{\text{min}}=\frac{mv^2}{4}}$. Below I give detailed analysis why this is so. My solution is in agreement with conservation of energy and I explain why energy is conserved. Also an explanation from purely dynamical considerations is given by calculating the tension of the carpet at the bending region.

First attempt. Let's consider how new elements of the carpet are brought into motion.

This increase doesn't happen abruptly by a jerk, so energy is not dissipated. To see this consider a wheel moving on a flat surface without slippage with constant speed $v/2$. 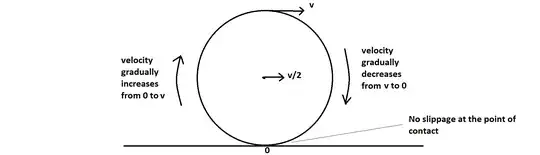If we go in the clockwise direction from the lowest point of the wheel, then the velocity of the points on the circumference gradually increase from $0$ to $v$ at the highest point, then gradually decrease to $0$ at the second half. This is well known, no jerking motion happens.

Similarly to the fact that energy is conserved for a wheel rolling without slippage the energy is conserved in the case of the carpet too: the work done by the pulling force $F\cdot 2L$ is converted into kinetic energy of the carpet $mLv^2/2$: $F\cdot 2L=mLv^2/2$, thus $F_{\text{min}}=mv^2/4$.

Second attempt. One might object that the bending of the carpet is not circular. In fact in the above reasoning this doesn't matter. But let's show this doesn't matter in another context too by calculating the tension of the carpet at the bending region.

We assume the bending curve has the same constant form at all times. When viewed in the reference frame moving with speed $v/2$ in the direction of the the external force $F$ this bending curve seems stationary. In this reference frame carpet 'flows' along this curve with constant speed $v/2$.

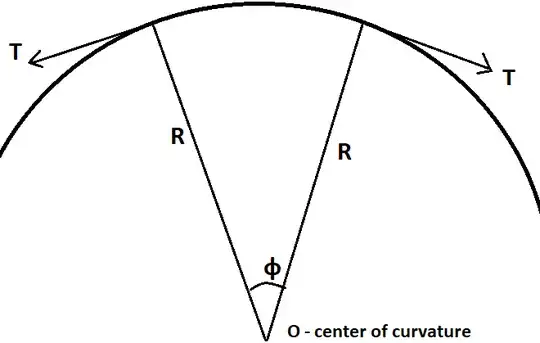
Now consider a certain element of this curve. Let $R$ be the curvature radius, $\phi\ll 1$ - the angle that this element is seen from the center of curvature. The length of the element and its mass is $mR\phi$. The tension if the carpet $T$ gives this element the centrifugal acceleration $\frac{v^2}{4R}$:

$$ T\cdot \phi=mR\phi\cdot \frac{v^2}{4R} $$

Thus $T=\frac{mv^2}{4}$ independent of the curvature.

Now we get the required minimal force that is needed to pull the end of the carpet with constant speed $v$: $F_{\text{min}}=T=mv^2/4$.

Is this analysis in agreement with conservation of momentum? There are two forces that act on the carpet as a whole in the horisontal direction: the pulling force $F$ and the friction force of the floor $F_{fr}$. If the carpet is not sliding along the floor then $F_{fr}=T=mv^2/4$. $F_{fr}$ acts in the same direction as the pulling force $F$. These two forces combined give the carpet the momentum $mLv$: $$(F+F_{fr})\cdot \frac{2L}{v}=(mv^2/4+mv^2/4)\cdot 2L/v=mLv$$ as required.

Third attempt. This is taken from the book https://www.amazon.com/200-Puzzling-Physics-Problems-Solutions-ebook/dp/B00E3UR79U . They get different answer from the two approaches above: $\color{red}{F_{\text{min}}=\frac{mv^2}{2}}$. Also they make a conclusion from this that half of the work done by pulling force is dissipated as heat.

(Solution in the book. They assume $m=1$, $L=1$.) "It seems tempting to try to find the minimum force required by using the conservation of energy, i.e. $F \cdot 2L = mv^2 /2$, where $L$ is the length of the carpet, ($L = 1$). The result would be $F =1/4$ , which is only one-half of the value calculated earlier. The error in this argument is to ignore the continuous inelastic collisions which occur when the moving part of the carpet is jerking the next piece into motion. Half of the work goes into the kinetic energy of the carpet, but the other half is dissipated as heat." (Quote from the book)

Answer 1

As expected, there has been a lot of discussion about this "puzzling" problem. No wonder that there have been many different solutions, most of them wrong and thus deleted, but nevertheless helpful in one way or another.

There is an issue about modeling the kink point of the carpet. The OP shows what would be the most intuitive way of doing it, by making the carpet bend along a half-circle rotating at speed $v/2$, also suggested by the image in the book your referenced.

Another result that is indisputable is that the total change in momentum in time is $\lambda v^2/2$. The total force acting on the upper segment must be this value. The question is how much of this force is attributed to the pulling force $F$. In the solution provided by the book, it seems to be all of it.

Following the OP, half of the force is a reaction to the static friction, in which case the correct answer is what is given already in the second attempt.

I was trying to model the bending point in such a may to get the total force to be responsible for the motion, but instead ended up with my other answer.

In conclusion, the pulling force seem to depend on how you model the joining point between the moving and the static part of the carpet. The OP gives the most intuitive answer.

Answer 2

I wish to address the ambiguous points which I think lead to the variety of different answers

1. We are given that the carpet is pliable, hence it is a reasonable approximation (I would even say that the authors of the problem are recommending this) to say that the radius of the bend (and the shape) are negligible.
2. I'm considering that the lower surface of the carpet (i.e. the parts which have not reached the bend yet) are stationary with respect to the ground, and the bend is moving with a velocity $\vec{v}$ with respect to the ground; this is something which was ambiguous some of the answers (if I recall correctly), but the diagrams provided suggest this. This also tells us about the friction in the system: the carpet's lower surface does not slide against the floor, and it is instead lifted upwards at the bend.
3. Furthermore, due to the small radius of the bend, the difference between the potential energy of a certain small section of the carpet before and after crossing the bend can be neglected.

These suggest my approach to the applicability of conservation laws in this problem: I think that they're largely unhelpful: the un-bent parts of the carpet are at rest with respect to an observer attached to the ground; they have no kinetic/potential energy. At the bend, a particle of the carpet is acted upon by a force which gives the particle an upwards velocity; after it is accelerated from rest over a small period of time, the particle moves at a constant speed $v$, with the direction changing until it reaches the rectilinear trajectory due to the central force stopping.

With this understanding in place, we can cautiously employ certain portions of the method from the solution manual. To avoid some ambiguity, let's use a different variable-naming convention: $\mu$ is the mass of $1\ \rm m$ of the carpet; $m(t)$ is the mass of the carpet which is in motion, and $\vec{v}$ is the velocity of the arts of the carpet which are considered in $m$. Considering the carpet to be sufficiently pliable, we can neglect the mass of the carpet which is not moving in the same direction as $\vec{v}$ (*).

Clearly, $m=\mu \vec{v} t$.

It is tempting to suggest that $$F=\frac{\mathrm{d}}{\mathrm{d}t}p=m\frac{\mathrm{d}v}{\mathrm{d}t}+v\frac{\mathrm{d}m}{\mathrm{d}t}=v\frac{\mathrm{d}m}{\mathrm{d}t}$$ which gives $F=v^2\mu$. However, it is not a correct approach as indicated in this answer. Instead, we can use the premise that if the work is $W=\frac{1}{2}m\vec{v}^2$,$$F=\frac{W}{s}=\frac{1}{2}m\vec{v}^2\times\frac{1}{\vec{v}t}=\frac{\mu \vec{v}^3t}{2\vec{v}t}=\frac{1}{2}\mu\vec{v}^2$$

If you want to make dimensional analysis difficult for your readers, you can feel free to replace $\mu$ with $m$ and switch back to the naming conventions from the question.

---

_{*this is acceptable with respect to conservation of energy: as mentioned earlier, those parts of the carpet are also moving with a speed $v$, and the direction doesn't affect the kinetic energy.}

Answer 3

After much struggling I have decided to go back to my simpler assumptions (for those who even still care about this problem anymore...)

---

Assumptions: I am going to assume that the bend in the carpet and any effects that might arise from it are negligible. I am also going to assume that whatever force is keeping the bottom section of carpet in place is not getting propagated to the upper section of carpet, since the bend is negligible.

I am going to model the system as a line element moving at speed $v$ relative to our frame that undergoes "continuous completely inelastic collisions" through addition of mass elements that are at rest relative to our frame.

---

Momentum:

We cannot use $$F=v\frac{\text d m}{\text d t}+m\frac{\text d v}{\text d t}$$ as explained here. The correct way to approach this equation is $$F+u\frac{\text d m}{\text d t}=m\frac{\text d v}{\text d t}$$ where $u$ is the velocity of the changing mass relative to the object whose mass is changing.

Therefore, we can model this system as something like a line mass, where it experiences a net external force $F$ and mass is being added to it at a constant rate $\frac{\text d m}{\text d t}$ with the relative velocity being $u$. In this case then $$F=-u\frac{\text d m}{\text d t}+m\frac{\text d v}{\text d t}$$

For us this becomes $F=-u\dot m$ for the upper section, since its center of mass moves at a constant speed. Since I am assuming no other forces acting on the upper section of carpet, $F$ is the force we are applying.

Since each part of the upper section of carpet moves at speed $v$ and each element that gets added to the carpet starts at rest, we have $-u=v$. The equation at the beginning of this answer becomes $$F=v\dot m$$

Now, $\dot m$ of the upper part is equal to $\frac{\text d}{\text d t}\lambda \left(\frac12 x\right)=\frac12\lambda v$, where $\lambda$ is the linear mass density of the carpet and $x$ is defined similar to what is in the provided "solutions" by the OP. Therefore

$$F=\frac12\lambda v^2$$

This agrees with the solutions only because we got lucky wiith how $-u=v$, but we have been more careful at applying $F=\dot p$ now.

---

Energy (Still wrong)

In considering energy, it is tempting to do the following: Say the upper section of carpet starts with no energy (due to no mass), and say that once $x=2L$ the entire upper carpet has kinetic energy of $\frac12Mv^2=\frac12\lambda LV^2$. Then, using the work-energy theorem with a constant force applied over $2L$, we get $$W=2FL=\frac12\lambda Lv^2$$ or $$F=\frac14\lambda v^2$$

However, the issue here is that these collisions are inelastic, so energy is being lost as mass is being added to the upper section of carpet. Therefore, we need to supply additional work to keep the carpet moving at a constant speed (with the kinetic energy then increasing due to the increase in mass).

Therefore, let us first consider the collision at some time of the carpet section of mass $m$ moving at speed $v$ and the additional mass $\text dm$ without the force being applied. Through momentum conservation we have $$mv=(m+\text dm)v_f$$ or $$v_f=\frac{mv}{m+\text dm}$$ where $v_f$ is the new velocity after the collision.

We know energy is lost, and the new kinetic energy of the system is given by $$K_f=\frac12(m+\text dm)v_f^2$$ therefore, we need to do some work $\text dW$ to get the speed up to what we want it to be. In other words: $$\text dW=\frac12(m+\text dm)v^2-\frac12(m+\text dm)v_f^2=\frac12(m+\text dm)(v^2-v_f^2)$$

Substituting in our expression for $v_f$ and doing some fun algebra (thanks Mathematica) we get to $$\text dW=\frac12\frac{(\text dm)^2+2m\text dm}{2(m+\text dm)}v^2$$

Since $\text dm\ll m$, we can neglect the $(\text dm)^2$ term in the numerator and the $\text dm$ term in the denominator. What we are left with is then $$\text dW=\frac12\text dmv^2$$

But from above we know that $\text dm=\frac12\lambda\text dx$, therefore, $$\text dW=F\text dx=\frac14\lambda\text dx v^2$$ or $$F=\frac14\lambda v^2$$

And I still can't get these to match.

Answer 4

I'll use a microscopic description of the carpet in order to find the value of the pulling force $F$ acting on the upper (moving) part.

First, imagine the carpet as a string of rigid bars of mass $\delta m$ and length $\delta l$ (with $\lambda = \delta m/ \delta l$) attached by hinges that are able to rotate up to an angle of 90 degrees.

The motion can be split in the following steps:

1. One bar is initially rotating around point $1$ with its extreme point $x$ moving with speed $v$ at time $t$, forming a right angle with the next bar.
2. This bar will thus engage the next one and the "L" shape will rotate around point $2$ by $90^{\circ}$ over a time $dt$ due to the pulling force $F$.
3. At this stage, the first bar will detach from the L shape and become part of the upper moving carpet, leaving the ($12$) bar behind rotating with speed $v$ at its end (point $1$). From here, we can continue our analysis by returning to the first step.

We can immediately get a couple of properties:

• Given that point $x$ moves with speed $v$, then $2 \delta l = dx = v dt$.
• The total momentum change is $d p = \delta m \, v = \lambda \, \delta l \, v = \frac{\lambda v^2}{2} dt$.

To find the force, I'll calculate the energy in two different ways:

1. Assuming a constant horizontal force $F$, the energy done on the system is $ \Delta E = 2 \, \delta l \, F$.

We need to calculate the rotational energy at time $t$. The process from 1. to 2. is an inelastic collision. Using conservation of angular momentum we can obtain the initial angular speed around point 2. Before engaging the next bar, the angular momentum of the vertical rod is $\frac{v \, \delta m \, \delta l}{3}$, which happens to be the same around point $1$ and point $2$. By engaging the next bar, one obtains an L shape with moment of inertia $I_L = \frac{5}{3} \, \delta m \, \delta l^2$. Solving for the angular speed one gets $\omega_0 = \frac{v \, \delta m \, \delta l}{3 I_L} = \frac{v}{5 \, \delta l}$.

2. The rotational energy gained per step is equal to $\Delta E = \frac{I_L}{2} ((\frac{v}{\delta l})^2 - \omega_0^2) = \frac{4 \, \delta m \, v^2}{5}$, where $\frac{v}{\delta l}$ is the angular speed at $t+\delta t$.

Equating these two expressions and solving for the force results in

$$F = \frac{2}{5} \lambda v^2$$

Note that the static friction force is the one keeping point $2$ in place during the rotation. This force does not do any work (as expected), yet it influences the required value of the pulling force $F$ in an indirect way by constraining the motion. Moreover, there is an inelastic scattering as an energy-loss mechanism.

Answer 5

In your first diagram you wrote

velocity increases from $0$ to $1$.

If this was happening then the carpet must be stretching in the curved region.

Due to the wheel rotating the rim of your wheel has a speed of $v$ and if the carpet is not slipping relative to the wheel then the speed of the carpet must change from zero to $v$ in the region of the point of contact of the carpet/wheel with the ground.
This is where the inelastic “jerking”, impulsive force acting, on a small section of the of the carpet occurs in your diagram.