Why is iron the peak of the binding energy per nucleon curve?

Question

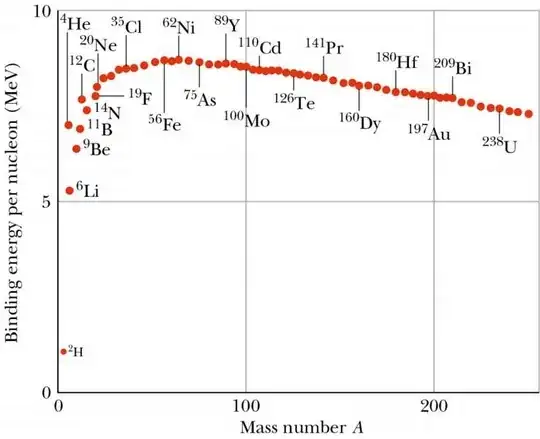
If Nickel-62 and Iron-58 have more binding energy per nucleon than Iron-56 does, then why is iron-56 shown as the peak of the binding energy per nucleon curve? Also, does adding neutrons always make the atom more stable because it will increase the strong nuclear force but not add any more electrorepulsive force?

Answer 1

From Wikipedia:

Iron-56 (56Fe) is the most efficiently bound nucleus meaning that it has the least average mass per nucleon. However, nickel-62 is the most tightly bound nucleus in terms of energy of binding per nucleon. (Nickel-62's higher energy of binding does not translate to a larger mean mass loss than Fe-56, because Ni-62 has a slightly higher ratio of neutrons/protons than does iron-56, and the presence of the heavier neutrons increases nickel-62's average mass per nucleon).

In any case, iron-56 is not necessarily usually shown (anymore) as the highest binding energy per nucleon, mostly because it's not usually possible to show the tiny difference in binding energy between iron-56 and nickel-62. The difference is so tiny that accounting for the fact that the neutron is 0.1% heavier than the proton, instead of treating all nucleons equally, changes which is bound more tightly. Because of this tiny difference, it's unlikely that you'll see one depicted as higher than the other on any plot that actually shows both of them, like this one (source: https://www.asc.ohio-state.edu/kagan.1/phy367/Lectures/P367_lec_14.html):

Can you tell which of the two has higher binding energy? I certainly can't.

In addition, adding neutrons does not always make the nucleus more stable. In the nuclear shell model, protons and neutrons, being distinguishable from each other, occupy distinct sets of energy levels in the nucleus. (As a side note, the neutron energy levels are shifted lower than the proton energy levels because there is no Coulomb repulsion among neutrons. This is why the heavier stable nuclei tend to have more neutrons than protons - you can fill more of the neutron energy levels for the same valence nucleon energy.) Since they're both fermions, you have to add new neutrons to higher and higher energy levels. Adding too many neutrons, enough to put the highest filled neutron energy level significantly above the highest proton energy level, will cause the highest-energy neutrons to spontaneously convert to protons via beta decay so that they can occupy a lower (proton) energy level.

Answer 2

1. The "folk wisdom" that iron-56 has the highest binding energy per nucleon is in fact incorrect; both iron-58 and nickel-62 have a higher binding energy per nucleon, with nickel-62 being the highest. I can't do much better than citing an article on the subject:

   M. P. Fewell, "The atomic nuclide with the highest mean binding energy". Am. J. Phys. 63, 653–658 (1995).

   The author of that work traces this misconception back to texts on stellar nucleosynthesis in the '50s and '60s. Stellar nucleosynthesis does favor the production of iron over nickel, and the author postulates that this fact may have been conflated with the peak of the binding energy curve.

2. We can roughly model nuclei as having a set of "proton energy levels" and "neutron energy levels". Since both protons and neutrons are spin-$\frac12$ fermions, this means that one can have at most two neutrons per energy level in the nucleus. Adding more neutrons to the nucleus will thus result in the neutrons being piled into higher-energy states.

   However, neutrons can undergo beta-decay into protons: $n \to p^+ + e^- + \bar{\nu}$. Suppose a neutron is in a relatively high energy level in the nucleus, and there is a vacant proton energy level below it. It can be energetically favorable for this neutron to turn into a proton and drop into this lower energy level. Thus, nuclei with too many neutrons will tend to undergo beta decay. (The same argument shows why nuclei with too many protons will tend to undergo either electron capture or inverse beta decay.)