I have a question concerning the LCDM spacetime diagram on this Physics Stack Exchange post.
How are the set of curves for $z = \text{constant}$ (1, 3, 10, 50, etc) constructed or calculated, i.e. what is the mathematical relation plotted in this comoving diagram?
To answer your question, we should think like this:
What is the proper distance to a galaxy which we observe as $z=1$?
Let us take the FLRW metric, $$\mathrm{d}s^2=-c^2\mathrm{d}t^2+a(t)^2[\mathrm{d}r^2+S_{\kappa}(r)\mathrm{d}\Omega^2].$$ For the path of light, we can write $$r=\int_{t_e}^{t_o}\frac {c\mathrm{d}t} {a}.$$
Now this integral has limit in time. But time is not an observable quantity in cosmology. Hence we should covert the integral limit to redshift by doing some calculations.
If we change the integral limit to redshift, the above integral becomes, $$r=cH_0^{-1}\int_{z_{now}}^{z_{emitted}}\frac {\mathrm{d}z} {E(z)}$$ for $$E(z)=\sqrt{\Omega_{\Lambda}+\Omega_m(1+z)^3+\Omega_r(1+z)^4+\Omega_{\kappa}(1+z)^2}$$ or we can use the simplified version, $$E(z)=\sqrt{0.69+0.31(1+z)^3}.$$
Now, to find the $r$ at $z=1$, we should simply set $z_{\text{now}}=0$ and $z_{\text{emitted}}=1$. Because at the time of emission, the desired $z$ should be $1$, and at the time of emission $z=0$.
So the result is $$r=cH_0^{-1}\int_{0}^{1}\frac{\mathrm{d}z}{E(z)} \\ =cH_0^{-1}\int_{0}^{1}\frac{\mathrm{d}z}{\sqrt{0.69+0.31(1+z)^3}}.$$
If you calculate the integral for, $c=3\times 10^8 \,\text{m}/\text{s}$ and $H_0^{-1}=4.4133353\times 10^{17}\,\text{s}$, $$r=10.73256352744068\,\text{Gly}.$$
So when the galaxy emits a light at a proper distance of $r=10.73 \,\text{Gly}$, the redshift value will be $z=1$.
For $z=3$, just change the integral limits and calculate the above integral and it would give you the proper distance for $z=3$.
To find the numerical solution of the above integral, you can use this site.
Note: Since we are taking $z_{\text{now}}=0$, proper distance = comoving distance.
Here are my findings for different z values,
$$z=1,r=10.73256352744068\,\text{Gly} \\ z=3,r=20.567781637223106\,\text{Gly} \\ z=10,r=30.486114555308745\,\text{Gly} \\ z=50,r=38.602145131495604\,\text{Gly} \\ z=1000,r=44.052504979871436\,\text{Gly}.$$
And the picture you shared is kind of confusing. I think this is better.
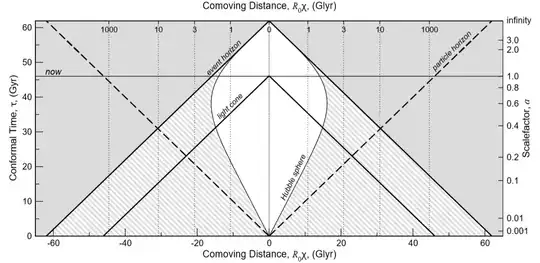
As we can see, the redshift values are fixed for a comoving coordinate, with respect to their current proper distances $r$, for $a(t_0)=1$.
