Retarded time and corresponding position

Question

EDIT: Added Clarification.

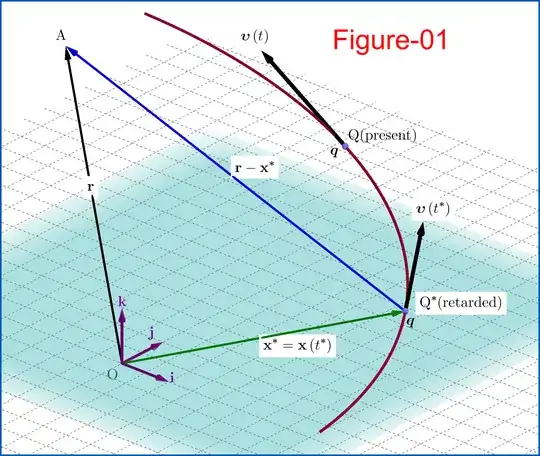
By various methods, it's possible to determine that in the formula for Electric potential for the position of a charge in uniform motion, $V=\frac{q}{4\pi\epsilon_0\kappa \cdot c(t-t_r)}$

Where $c(t-t_r)$ is the distance between field point and charge at the retarded time, and $\kappa=1-\frac{\vec{\beta}\cdot (\vec{x}-\vec{u}t_r)}{c(t-t_r)}$

$\vec{\beta}$ is velocity divided by c. The position of the charge at a given time $t$ is $\vec{u}t$

and the following equalities hold.

$$D=\sqrt{(x-ut)^2+(y^2+z^2)/\gamma^2}$$

where $\gamma=\frac{1}{\sqrt{1-\beta^2}}$ and $\beta=u/c$, where $v$ is the uniform velocity of the charge.

Also, $D=c(t-t_r)-\vec{\beta}\cdot(\vec{x}-\vec{u}t_r)=\kappa c(t-t_r).$

Now $D$ is not the distance between the field point $\vec{x}$ and the charge at retarded time $\vec{u}t_r$. Yet $V=\frac{q}{4\pi\epsilon_0D}$.

How is one to interpret $D$?

As a commenter suggested, it might be better to consider the change happening to the charge. Instead of $q$ we have $q_{eff}=q/\kappa$ and use the retarded time distance in the denominator $V=\frac{q_{eff}}{4\pi \epsilon_0\cdot c(t-t_r)}$.

Now the distance used makes sense, it's the distance to the charge between the field point and the charge location at the retarded time. But what is the physical meaning of this adjusted charge? While it makes the math work and allows for the use of a physically meaningful distance in the formula, it introduces additional questions. What is the physical meaning of adjusting the charge like this? A charge is a Lorentz invariant and $\kappa \neq \gamma$.

That the formula takes this form can be explained by the need to rescale the charge density and component of displacement in the direction of motion, but this fails to explain the new formula in terms of the retarded time.

Answer 1

The meaning of D:

Determination of the field produced by a charge e moving with a uniform motion V .

Assuming that the charge is at the origin of the coordinates of the frame of reference K' and that the latter moves with respect to K parallel to the x-axis, i.e. y=y', z=z'

At the time t=0, the origins of the two reference frames are merged. it follows that in the reference frame K the coordinates of the charge are $x=vt, y=z=0$. In the K' frame of reference, we have a constant electric field of vector potential $A'=0$ in K' and scalar potential $V'=\frac{e}{R'}$, where $R'^{2}= x'^{2}+y'^{2}+z'^{2}$.

In the K reference frame, we have from the LT for the field :

$V=\gamma V'=\frac{e}{R'\sqrt{1-\beta^{2}}}\;\;\;,$ to simplify the writing $1/4\pi\epsilon_{0} \sim 1$

From the LT:$ \;\;R'^{2}=\gamma^{2}[(x-vt)^{2}+\gamma^{-2}(y^{2}+z^{2})]$

$D^{2}=\gamma^{-2}R'^{2}=(x-vt)^{2}+\gamma^{-2}(y^{2}+z^{2}) $

$D=\sqrt{1-\beta^{2}}R'$

See volume II: Field theory L.Landau, E.Lifchitz

Answer 2

---

Under a general smooth curvilinear motion of the charge $\;q$, see above Figure-01, the scalar electromagnetic potential is given by \begin{equation} \phi(\mathbf r, t)\boldsymbol{=}\dfrac{q}{4\pi\epsilon_0}\dfrac{1}{\left\Vert\mathbf{r}\!\boldsymbol{-}\!\mathbf{x}^{\boldsymbol{*}}\right\Vert\!\boldsymbol{-}\! \dfrac{\:\boldsymbol{\upsilon}^{\boldsymbol{*}}}{c}\boldsymbol{\cdot}\left(\mathbf{r}\!\boldsymbol{-}\!\mathbf{x}^{\boldsymbol{*}}\right)}\boldsymbol{=}\dfrac{q}{4\pi\epsilon_0}\dfrac{1}{\left[1\!\boldsymbol{-}\! \dfrac{\:\boldsymbol{\upsilon}^{\boldsymbol{*}}}{c}\boldsymbol{\cdot}\dfrac{\left(\mathbf{r}\!\boldsymbol{-}\!\mathbf{x}^{\boldsymbol{*}}\right)}{\left\Vert\mathbf{r}\!\boldsymbol{-}\!\mathbf{x}^{\boldsymbol{*}}\right\Vert}\right]\cdot\left\Vert\mathbf{r}\!\boldsymbol{-}\!\mathbf{x}^{\boldsymbol{*}}\right\Vert} \tag{01}\label{01} \end{equation}
where the superscript $\;^{\prime}\boldsymbol{*}^{\prime}\;$ refers to the retarded quantities time, position and velocity $\,t^{\boldsymbol{*}},\mathbf{x}^{\boldsymbol{*}},\boldsymbol{\upsilon}^{\boldsymbol{*}}\,$ respectively. Above equation could be expressed as \begin{equation} \phi(\mathbf r, t)\boldsymbol{=}\dfrac{1}{4\pi\epsilon_0}\dfrac{q}{\kappa\cdot R} \tag{02}\label{02} \end{equation} where \begin{equation} R\boldsymbol{=}\left\Vert\mathbf{r}\!\boldsymbol{-}\!\mathbf{x}^{\boldsymbol{*}}\right\Vert \tag{03}\label{03} \end{equation} is the distance from the retarded position of the charge $q$ (point $\rm Q^{\boldsymbol{*}}$ in the Figure) to the field or observation point (point $\rm A$ in the Figure) and \begin{equation} \kappa\boldsymbol{=}1\!\boldsymbol{-}\! \dfrac{\:\boldsymbol{\upsilon}^{\boldsymbol{*}}}{c}\boldsymbol{\cdot}\dfrac{\left(\mathbf{r}\!\boldsymbol{-}\!\mathbf{x}^{\boldsymbol{*}}\right)}{\left\Vert\mathbf{r}\!\boldsymbol{-}\!\mathbf{x}^{\boldsymbol{*}}\right\Vert}\boldsymbol{=}1\!\boldsymbol{-}\! \dfrac{\:\boldsymbol{\upsilon}^{\boldsymbol{*}}}{c}\boldsymbol{\cdot}\mathbf{n}_{_R} \tag{04}\label{04} \end{equation} is a positive factor less than or equal to or greater than 1 if instantaneously the charge $\;q\;$ from its retarded position $\rm Q^{\boldsymbol{*}}\;$ is coming closer, is running away or keep the same distance from the field point $\rm A$ respectively.

Now, to interpret the result \eqref{02} in the frame of electrostatics you define an effective distance \begin{equation} R_{\rm eff}\boldsymbol{\equiv}\kappa\cdot R \tag{05}\label{05} \end{equation} and conclude that the scalar potential is that of the electrostatic one due to the presence of the charge not at the real distance $R$ but at a distance $R_{\rm eff}$ \begin{equation} \phi(\mathbf r, t)\boldsymbol{=}\dfrac{1}{4\pi\epsilon_0}\dfrac{q}{R_{\rm eff}} \tag{06}\label{06} \end{equation}

But I think that a more suitable interpretation would be to define an effective charge \begin{equation} q_{\rm eff}\boldsymbol{\equiv}\dfrac{q}{\kappa} \tag{07}\label{07} \end{equation} and conclude that the scalar potential is that of the electrostatic one due to the presence of a particle at the real distance $R$ not with the real charge $q$ but with the effective charge $q_{\rm eff}$ \begin{equation} \phi(\mathbf r, t)\boldsymbol{=}\dfrac{1}{4\pi\epsilon_0}\dfrac{q_{\rm eff}}{R} \tag{08}\label{08} \end{equation}

These results have nothing to do with the time dilation and length contraction effects.

---

Related : Retarded time miscalculation?