Experimental limits on non-Newtonian gravitational force at length scales larger than 1 meter?

Question

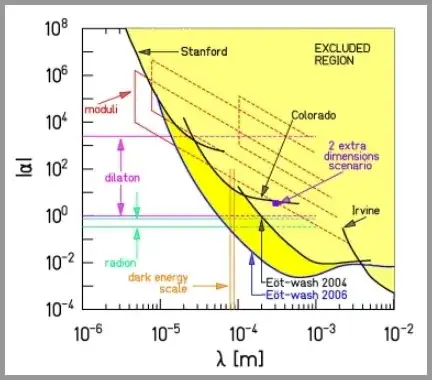
This answer from 2012 shows some information on an exponential term characterized by relative strength and range parameters $\alpha$ and $\lambda$,

One potential tested here is here $$V(r)=-G\frac{m_1m_2}{r}(1+\alpha\exp(-r/\lambda))$$

The below plot shows the exclusion limits for both parameters $\alpha$ and $\lambda$

but the largest length shown is only about a centimeter.

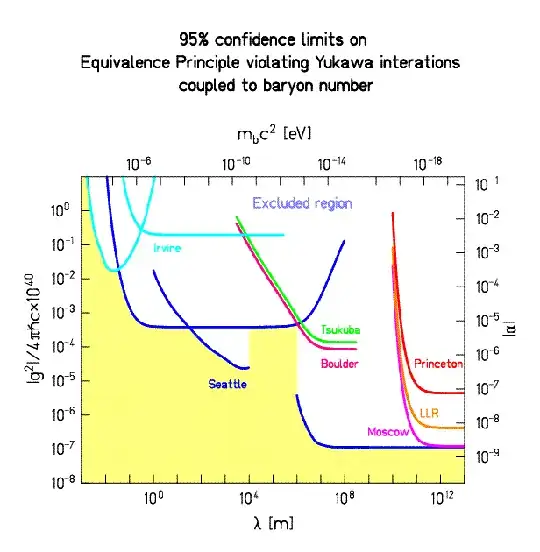
Going to the University of Washington's page The Eöt-Wash Group; Results, I can see the following plot of limits that includes range scale of 1 meter and above:

but I can not understand the physics or the units.

Question: Are there any experimental limits on non-Newtonian gravitational force at length scales larger than 1 meter? Is there some way to know current limits on non 1/r potential between say 1 meter and 1 AU?

---

update: This has the unit-less expression I seek and the length scale of 1 meter and larger, but the experiment is based on a "material-composition dipole pendulum" torsional balance; one side of the dipole is four beryllium masses, and the other is four titanium masses.

That's a specific type of short-range deviation. I'm looking for a limit on all possible sources. Perhaps none exists yet?

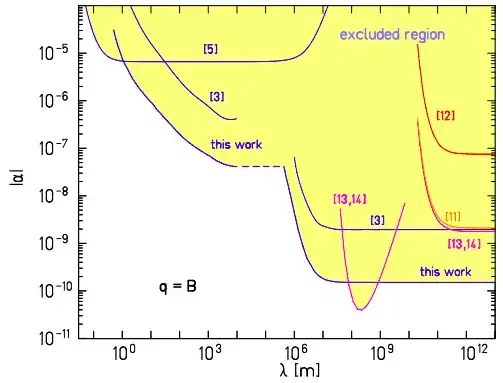
From "Test of the Equivalence Principle Using a Rotating Torsion Balance," Schlamminger et al., PRL 2008, also on arXiv:

FIG. 3: New upper limits on Yukawa interactions coupled to baryon number with 95% confidence. The uncertainties in the source integration is not included in this plot. The numbers indicate references. The shaded region is experimentally excluded. Preliminary models for 10 km < λ < 1000 km indicate that the limit on α is smaller than the dashed line.

Answer 1

You seem to be asking whether there are equivalence-principle tests for long-range non-Newtonian gravity, but not tests for long-range non-Newtonian gravity which are independent of composition. (Set aside for the moment the detail that general relativity is a well-tested non-Newtonian theory of gravity; we're asking here about new interactions in the weak-field limit.)

The issue is that the Yukawa potential,

$$ V(r) = \frac{-G m_1 m_2}{r} \left( 1 + \alpha e^{-r/\lambda} \right) $$

only gives you interesting dynamics for separations where $r$ is comparable to $\lambda$. In the long-distance limit $r \gg \lambda$, the exponential $e^{-\text{large}}$ sends the correction to zero, and you recover the $1/r$ potential. But in the short-distance limit $r \ll \lambda$, the exponential $e^{-\text{small}}$ has a nonzero constant value, and you also recover the usual $1/r$ potential — just with a different effective coupling constant, $G \to G(1 + \alpha)$. And the gravitational constant $G$ has turned out to be terribly difficult to measure; the last I read, there were two high-quality laboratory measurements that were not consistent with each other. Note that we know $G$ to a few parts in $10^{-5}$, probably from a fits-in-a-room Eötvös-type experiment with independently measured masses, and the meter-scale limits on $\alpha$ are right around $10^{-5}$: it's the same information. In the short-range experiments the constraints on $\alpha$ get weaker and weaker until you get to $10^{-15}$ meters and have to include the Yukawa potential due to the pion.

If your interest is in gravitation on length scale longer than $10^7$ meters, you have to leave Earth. Putting a satellite with good telemetry in orbit around an object with mass $M$ lets you get a very good measurement of the product $GM$, but not $G$ or $M$ separately. (The Particle Data Group reference lists the Sun's theoretical Schwartzchild radius, $2GM_\text{sun}/c^2$, to fifteen significant figures, but its mass $M_\text{sun} = G M_\text{sun}/G$ has the same fractional uncertainty as $G$.) The last real challenge to Keplerian orbits within the solar system was probably the "Pioneer anomaly," but that was recently explained as a thermal radiation effect, and I'm not sure that it was ever really discussed in the language of a Yukawa potential. Possibly also related (but probably not) is the flyby anomaly.

As to whether these experiments test gravity or some other force: I think that's an intellectual distinction. What we measure in experiments is what happens. We like to look at satellites staying in orbit and tell ourselves "that's happening because of gravity," and look at nuclei undergoing beta decay and tell ourselves "that's happening because of the weak charged current," but the reality is that all of the things are happening all of the time, and we distinguish among them for our own convenience. If we were to discover a non-$1/r$ correction to weak-field gravity, whether there was an equivalence principle violation or not, we would have a lot of work to do to understand why. And because the measurement techniques for all of these precision long-range new-force searches are similar, then the literature overlaps.