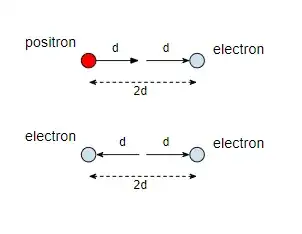
I'm not studying physics, I was just curious that if the electric field created by electron and positron in a dipole follows the same rules as double slit experiment. That is, for example on the midpoint, the field should be the sum of two separate fields, is the field energy 4 times higher than that of the single electron? (2 times higher than the sum of individuals). Does this mean that if another electron is put in between, it is four times likely that it hits a photon?
Then in the mentioned scenario can't we measure which one interacted with the other electron?
If we can't why, and if we can shouldn't the field energy be half? (Is it like: interacting with one + the pair attracting each other = interacting with the other one)