Intuition behind dual vectors ('Bongs of a bell' does not help)

Question

Similar to the post here (How to visualize the gradient as a one-form?), I'm wondering about an intuition behind dual vectors and differential forms (and the link in that answer to Thorne's notes is broken now). I'm not as familiar with level sets (as mentioned in post above), and both Carrol and MTW leave the explanation somewhat wanting... MTW's "bongs of a bell" explanation is particularly useless, and not having quantum mechanics experience means that "kets" and "bras" is not helpful either. Am I just unprepared for the material? I didn't think QM was a prereq for GR...

Is there an intuitive explanation for the relationships between vectors, their duals, and a geomretic object they describe? One of the key differences between vectors and their duals seems to be that dual vectors are reliant on the metric. It's also clear that dual vectors occupy a space of the same dimensionality as the vectors and can function on a geometric object to return its components in the 'original' vector space.

As an example, we know the dual vector $\overline{w}^1$ acts on $\overrightarrow{v}$ as $\overline{w}^1 \overrightarrow{v} = v^1$, is that equivalent to $\overline{w}^1 g_{aa} v^a = v^1$ ? Or does the dual vector act on $\overrightarrow{v}$ in another way?

Answer 1

Dual vectors are a notion independent from presence of the metric: in fact, a dual vector is simply any linear functional that operates on a vector space (on some field $\mathbb K$) and gives as a result a number in the field $\mathbb K$;

As a very low-profile example, think about a matrix $n\times1$ (visually, a column vector); the set of all matrices of this kind form a vector space $V$ with the usual notions of sum of matrices and multiplication by a scalar;

A linear functional on this space is a matrix $1\times n$, acting on any vector of $V$ by means of the usual matrix-matrix multiplication: the result is indeed clearly a scalar (real or complex depending on the field of the vector field and the components of the linear functional) and you can verify that the action is linear.

Surely, if you have a metric space, you can define an isomorphism between vectors in your vector space and vectors in the dual space, by the identification

$$v\in V,\, v=v^a e_a,\Rightarrow \bar v=\bar v_a e^a,\, \bar v_a=g_{ab}v^b$$

Where with $e_a$ I mean any basis of the vector space $V$ and with $e^a$ the corresponding dual basis of the dual vector space $V^D$, defined as the set of linear functionals such that

$$e^a(e_b)=\delta^a_b$$

Answer 2

Suppose you're going to buy some flour and sugar. You can represent the amount of flour and sugar as a two-dimensional vector: one component says how much flour you're buying, and the other says how much sugar. If you want to know how much money you need, you need to know the prices. That, too, can be represented by a two-dimensional vector. We can think of price as being the result of combining these two vectors by taking, for each substance, the price of that substance times the amount of that substance, and then adding up the result of all those multiplications.

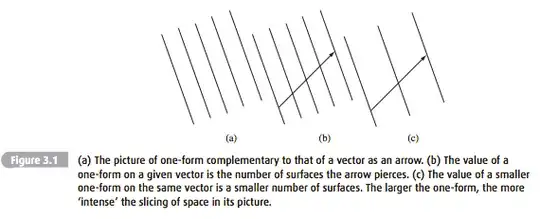
Suppose we're given any vector space with finite dimension $n$. By definition of "dimension", there is some set of $n$ vectors $v_1, v_2 ...v_n$ that forms a basis for that space. If we want to take each vector to a scalar, then we have some function $f:$v$\rightarrow c$, where v is a vector and $c$ is a scalar. If $f$ is linear, then it is uniquely determined by its actions on the basis vectors: if we know $f(v_i)$ for all $i$ from 1 to $n$, then we know $f(v)$ for any $v$. That means that $f$ can be characterized by a list of its outputs: if we have $[f(v_1),f(v_2)...f(v_n)]$, then we know what $f$ is. So if we think of a vector as "a list of n numbers", then $f$ is acting like a vector. This is what the dual space is: it's the set of all linear functions from a vector space to the set of scalars. The dual space is itself a vector space, and the original vector space acts as the dual of the dual: that is, instead of thinking of each member of the dual space as a function acting on the original vectors, we can think of the original vectors as functions acting on the dual vectors. So given $v$ and $f$, $v(f)$ gives a scalar. So the original space and the dual space act in isomorphic ways: one can be considered to be acting on the other. Furthermore, they have the same dimension, thus they are the same "size" in some sense, and we could, if we wanted, "pair" each vector in one with a vector in the other.

Of course, a list of prices or quantities of flour and sugar is much different from a relativistic vector. Such a list doesn't represent anything in spacetime, and each component represents something completely different, while the components in relativity are supposed to be related through transformations such as rotations and Lorentz transforms. And prices and quantities represent completely different things. So even though we could pair of quantities with a set of prices, that pairing would be arbitrary: there would be lots of different ways of doing it. We could have a pairing that pairs a pound of flour with 1 dollar/pound. Or we could have a pairing that pairs an ounce of flour with 1 cent/ounce, to take just two examples.

Now suppose we want an operation that takes two elements of the original space, and gives a scalar as output. One way of defining that would be to take the vector that is paired with the first, and apply it to the second. That is, suppose we're given vectors $u$ and $v$ that are both in the original space. We could find what vector in the dual space is paired with $u$, and then apply that to $v$. But remember, the pairing is arbitrary. So we need something that tells us what pairing we're using. That's where the metric comes in. The metric is often given as a function that takes two elements of the original space and gives a scalar as output: $g: (u,v) \rightarrow c$. But it can also be thought of as a function that take a member of the original space as input and gives a member of the dual space as output. It's not quite accurate that the dual vectors are reliant on the metric, but their relationship to the original space is.

Answer 3

Since no one has explicitly mentioned Schutz's explanation in A First Course in General Relativity I will outline it, as it is particularly intuitive:

As others have mentioned, dual vectors/one-forms/covectors can be seen as a map from a vector to a scalar (and in general, covariant n-th order tensors map contravariant n-th order tensors to scalars and vice versa). In index notation this is just $s=w_iv^i$

Visually, vectors can be neatly represented as an arrow–an object with direction and magnitude–and naturally then level sets map these arrows to scalars by counting the number of rungs the arrow crosses. You have probably seen level sets before; think topographic maps showing elevation–each rung represents some set height.

Page 62 of Schutz has the following figure which summarizes: