What is the physical meaning of retarded time?

Question

Consider this figure

Now, when I measure a field produced by the charge $e$ at the point $\mathbf r$, at the time $t=t_1$, it means that the charge sent the signal field at the time $t=t_r$, where $t_1$ and $t_r$ are related by $$t_{r}=t_1-\frac{||\mathbf{r}-\mathbf{r}_{e}(t)|{}_{t=t_{r}}||}{c} $$ Now, my question is, how is it possible that we can take $t_r$ like a time variable? I mean, when we want to measure the velocity of the charge $\mathbf v_e$, I must derive $\mathbf r_e$ respect to $t_r$: $$\mathbf{v}_{e}=\frac{d\mathbf{r}_{e}}{dt_{r}}$$ but why? I mean, why not to derive respect to $t$? So, what is the physical meaning of $t_r$? Or, in other words, how can we interpret the time $t_r$? Are there actually two time-axes?

Answer 1

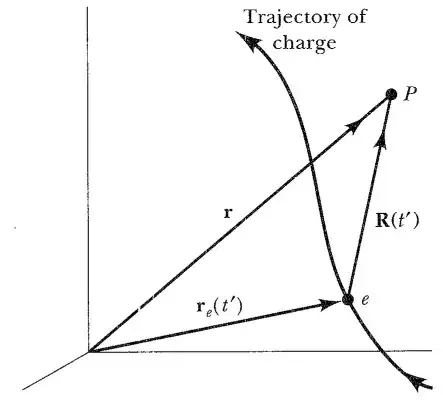
This is the usual argument for explaining retarded time -

Consider a charge moving with a constant velocity along a straight line. If the charge suddenly comes to a halt, there will be a change in the electric field due to the acceleration. But this change in the electric field isn't communicated instantaneously through the whole universe, that's prohibited by special relativity and the finite travel time of light.

Therefore one has to infer that observers that are closer to the charge "see" the change in the field earlier than observers farther away.

What that means for an observer too far away to see the change is this - If you are calculating a current/some other property dependent on the velocity of the particle, you have information that is old. The particle has already stopped moving, but you just haven't seen it as yet. So to get the physically accurate picture in the frame of the particle, you have to use retarded time, because otherwise you will infer that the particle is still moving at a constant velocity now. But you don't possess that information. You only know that it was moving at time $t - \frac{r}{c}$ earlier, so all calculations about the state of the system must be carried out with respect to that time.

So to answer your questions : $t_r$ is a time variable because it still depends on t $$t_r = t - \frac{r}{c}$$ which is clearly dependent on $t$. It isn't that you have two time axes, you are just evaluating your system at a finite point in the past (i.e., $t_r \leq t$ always).

Answer 2

The idea is that it takes time for a signal to travel from a source to where it is being observed--so the field here and now doesn't depend on the charge distribution now, it depends on the value that the charge distribution had $t - \frac{\ell}{c}$ ago, since information cannot travel instantaneously.

Answer 3

Radar uses the principle of retarded time to calculate distances

Since $x=ct$, $dx =c dt$! Define $dx=x_1-x_2$. If $x_1$ - radar location and $x_2$ -target location, $dt=dx/c=(x1-x2)/dt$ where $dt$ is the time required to travel to target! So round trip time $=2 dt$ which is recorded by electronic clocks. This is an example of retarded time not special relativity ;SR involves time dilation In SR $t'=t/(\sqrt{1-v^2/c^2}$ where $v$ (velocity) can never reach $c$ and when $v<<c$, $t'=t$. I have yet to see a good derivation of retarded time versus $t'$.