Can a battleship float in a tiny amount of water?

Question

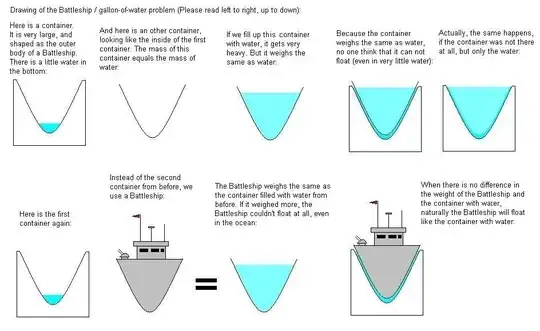
Given a battleship, suppose we construct a tub with exactly the same shape as the hull of the battleship, but 3 cm larger. We fill the tub with just enough water to equal the volume of space between the hull and the tub. Now, we very carefully lower the battleship into the tub.

Does the battleship float in the tub?

I tried it with two large glass bowls, and the inner bowl seemed to float. But if the battleship floats, doesn't this contradict what we learned in school? Archimedes' principle says "Any floating object displaces its own weight of fluid." Surely the battleship weighs far more than the small amount of water that it would displace in the tub.

Note: I originally specified the tub to be just 1 mm larger in every direction, but I figured you would probably tell me when a layer of fluid becomes so thin, buoyancy is overtaken by surface tension, cohesion, adhesion, hydroplaning, or whatever. I wanted this to be a question about buoyancy alone.

Answer 1

Yes it floats. And it has displaced its "own weight of water" in the sense that if you had filled the container with water and only then lowered the ship into the container, nearly all that water would have been dispaced and is now sloshing around on the floor.

Answer 2

Note that the water does not need to have been present - this calculation gives just the way to calculate the non water volume occupied by the floating object (that hence is unavailable for water).

So in your example, assume you put the ship into the container. If you filled it up to the same water level without the ship being present - that is the displacement caused by the ship.

 BBB
wBBBw     wwwww     w   w
wBBBw vs. wwwww NOT w   w
wwwww     wwwww     wwwww

In this sketch, 6 w have been "displaced".

Hence your example works even with a tiny gap. You can argue that hydraulic machines work with 0 gaps. The piston is the boat in the cylinder.

Answer 3

The USS Missouri $5.8 \times 10^7\,\rm kg, \, 270\,\rm m$ long with a fully laden draft of $11.5\,\rm m$ has an underwater surface area in excess of $270\times 11.5\times 2 \approx 6200\,\rm m^2$ and needs to "displace" $5.8 \times 10^7\,\rm kg$ of salt water (density $\approx 1020 \,\rm kg \, m^{-3}$) to float.

Assume a custom made tank so that an even thickness of water (total volume $1 \,\rm litre = 0.001 \,m^{-3}$) surrounds the USS Missouri below its waterline.
This thickness of the water layer would be smaller than $\frac{0.001}{6200} \approx 1.6 \times 10^{-7} \rm m$.

So in theory possible but in practice very highly unlikely.

---

The OP has changed the title from "1 litre" to "a small amount of water".
All that needs to be done is to choose a volume of water such that it is practically possible to float the USS Missouri in a suitably shaped dock and the OP's layer of water 3 cm thick might be possible in practice?

The picture in this answer gives a flavour of an "apparent lack of water" being able to float a ship.

Answer 4

The issue is just in your "definition" of displaced. When we say "the buoyant force is equal to the weight of the displaced fluid" (which is more true than it seems people are saying it is), displaced does not mean "how much fluid overflows out of our container" (unless we started with a full container).

The displaced fluid really just means how much fluid is pushed out of the way. What this leads to is that whatever volume of the object is submerged under the fluid surface, this is the volume of the fluid displaced. If we were to calculate the weight of this volume of water, we would find that it is equal to the buoyant force exerted on the object.

Therefore, in your example, if the volume of the boat that is submerged would give a volume of water that weighs the same as the boat, then the boat will float. How you get to this final configuration is irrelevant.

As a counter example to using the idea of water spilling out of a container, just imagine a boat in the ocean, where no water is spilling out of a container, yet the boat still floats.

Answer 5

The question you ask is a good one, and a common one. The phrasing of Achimedes' principle you use is most apropos in situations where you have a large body of water compared to the size of the vessel, so that you don't noticeably raise the water level.

The full mathematical phrasing of the principle holds true in all of these situations.

If your boat meaningfully increases the water level, like it must in your example, you have to play some mental gymnastics with the definition of "displace" to arrive at the correct answer. That's not to say that Archimedes' Principle is wrong, just that the informal phrasing gets a bit tricky to apply. The formal version, involving moving water upwards against the pull of gravity, does not run into any such complications.

Answer 6

Like other answers have said, the issue comes from an incorrect understanding of "displaced".

Imagine you lie in a bathtub. Now you fill up the bath until it covers your legs and body (not your head). Your body is very slightly less dense than water, so you verrrry slightly float - maybe only a few mm, not much, and probably still touching the sides and bottom of the tub.

There was never any water where your body is. The water filled the tub around you.

Then, the "displaced water" is the water that would have been in the tub, if your body vanished and enough water was added to keep the surface level of the water at the same level.

What Archimedes is saying us that, if the tub was so big that you floated (without moving) and you weren't touching the sides or bottom, then your body's level in the water is set at the level which displaces the same mass of water. That "missing" water doesn't need to have been there originally (see definition above).

Going in the other direction, imagine I trim the bathtub until it's1/2 an inch from your body in all directions, and you're still floating. The amount of water is tiny. What matters is (as above) the among of "missing" water where your body is, that would be below the surface level of the water. Not the remaining water around you in the bath.

Answer 7

For the interested, here is a little illustration I made once, to defend someone called 'Marilyn vos Savant'.
I didn't believe what people wrote in there against her statement, about a battleship floating in a bucket of water.
I am very happy to see, that everybody in here knows what is right.
Here is the illustration:

Answer 8

As the battleship is placed in the giant tub, the water along the sides rises to a height, h. This produce a pressure = water density x 9.8 x h in the thin layer of water beneath the ship. This pressure x the area of the bottom of the ship equals the weight of the ship, so it floats. If, instead of a giant tub, we place the ship in the ocean, h is achieved not by the water rising, but the ship descending to an equilibrium depth (hopefully less than the distance between the ship’s bottom and the deck).