Another objection to Feynman's moving infinite sheet of charge "radiator"

Question

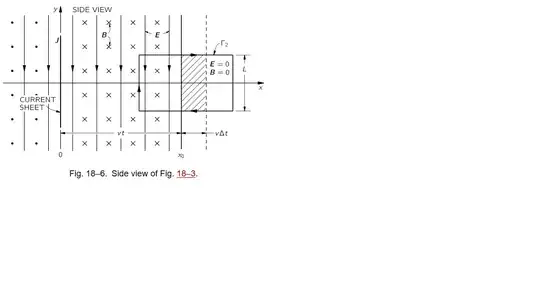
In The Feynman Lectures on Physics Vol II 18-4, A travelling field we are provided the thought experiment of two uniformly and oppositely electrically charged planar sheets of infinite extent lying in close proximity. The charge densities are equal in magnitude so that their net charge is zero. Let one lie in the $Y\times{Z}$ plane and the other lie indistinguishably near the first. The positively charged sheet is instantaneously set in motion parallel to itself at a constant speed in the positive $Y$ direction.

The assertion made by Feynman is that this sets up a surface current density which induces a magnetic field which propagates away from the charged planes and in so doing induces an electric field pointing in the negative $Y$ direction.

I understand why this might seem like a useful model. I was at first confused about the persistence of the electric field behind the wave-front. I posted about that Feynman Lectures Vol II-18 A travelling field: I'm not getting Feynman's result a while back.

But now I have another objection. According to Vol II 13-6 The relativity of magnetic and electric fields the magnetic field induced by an electric current is actually a result of relativistic length contraction. The conducting wire considered in 13-6 is supposed to be neutrally charged in its rest frame. When a test charge moves along the direction of the wire, the apparent charge densities of the wire's stationary positive charges and moving negative charges become different due to differences in their motions relative to the test charge.

For example, if the test charge moves with the average velocity of the conducting electrons, the conduction electron density is decreased from that of the wire's rest frame by a factor of $1/\gamma$, since relative to the wire's rest frame the conducting swarm appears length contracted. The positive charge density of the wire minus the conducting electrons appears to the test charge to be increased by a factor of $\gamma$ because it appears length contracted.

In the case of the charged sheets, before set in motion, the "conduction" charges have the same rest density as the "neutralizing" charges of the sheet that remains at rest. Once set in motion, the moving sheet become length contracted relative to the initial rest frame. Since the magnetic effect of current has already been shown to be a purely relativistic result, it seems impossible to neglect it by arguing that we are dealing with "non-relativistic velocities".

By the above reasoning, I conclude that once the "conducting" sheet is in motion, in the initial rest frame there will be a non-zero $X$ component of the electric field. I have yet to figure out how the $-Y$ component of the electric field can be accounted for using the relativistic approach of 13-6.

Is my understanding of this correct in so much as there should be a $X$ component of the electric field produced by the pair of sheets once the "conducting" sheet is set in motion? How might the $-Y$ component of the electric field advertised by Feynman be accounted for using the approach of 13-6?

Answer 1

How might the −Y component of the electric field advertised by Feynman be accounted for using the approach of 13-6?

It can't be. Don't be fooled into thinking that all electric and magnetic fields are due to the length contraction of some charge distribution or another. The fact that electric and magnetic forces mix together when you change reference frame does not mean that there's no such thing as magnetism or induction under careful scrutiny (as should be obvious - magnetic fields can exist in the absence of any charges at all).

Is my understanding of this correct in so much as there should be a X component of the electric field produced by the pair of sheets once the "conducting" sheet is set in motion?

Yes - however, this accounts for a contribution to the total electric field on the order of $\frac{u^2}{c^2}$ (where $u$ is the velocity of the current sheet), which can be neglected in the limit of small $u$ when compared to the inductive electric field, which is much larger.

As Feynman notes, magnetic field (in the nonzero region) is given by

$$\mathbf B = -\frac{J}{2\epsilon_0 c^2}\hat z = -\frac{\sigma' u}{2\epsilon_0 c^2} \hat z = -\frac{\sigma u}{2\epsilon_0 c^2} \hat z + \mathcal O\left(\frac{u^3}{c^3}\right)$$ where $\sigma$ is the surface charge density on the plane, and $\sigma'$ is the Lorentz-contracted surface charge density. The induced electric field is then $$\mathbf E = -c|\mathbf B|\hat y = -\frac{\sigma' u}{2\epsilon_0 c} \hat y = -\frac{\sigma u}{2\epsilon_0 c} \hat y + \mathcal O\left(\frac{u^3}{c^3}\right)$$ To lowest order in $u/c$, we can simply replace $\sigma'$ with $\sigma$ in both expressions.

On the other hand, the $\hat x$-component of the electric field which can be attributed to the Lorentz-contraction of the moving charge distribution is

$$\mathbf E' =\left( \frac{\sigma'}{2\epsilon_0}-\frac{\sigma}{2\epsilon_0}\right)\hat x = \left[\frac{\sigma}{2\epsilon_0}\left(\frac{1}{\sqrt{1-u^2/c^2}}-1\right)\right] \hat x = \left(\frac{\sigma}{2\epsilon_0}\frac{u^2}{c^2}\right) \hat x + \mathcal O\left(\frac{u^4}{c^4}\right)$$

It would be an interesting exercise to include this higher-order component of the electric field in the self-consistent analysis performed earlier in Feynman's derivation; I think you'd find that the wave would propagate outward at slight angle (not directly along the x-axis) and that there would be an additional higher-order contribution to the magnetic field in a direction other than $\hat z$.

In any case, to lowest order in $u/c$ (i.e. the limit of small velocities), the electric field is simply equal to the inductive contribution.

---

You're not wrong to be concerned about the idea of throwing away small terms; after all, if a particle is moving with a speed $v \sim u$, then the magnitude of the magnetic force on the particle is comparable to the electric force due to the previously-neglected electrostatic field. However, both of those forces are $u/c$ times smaller than the force due to the inductive electric field, and so as long as we are only working to lowest order in $u/c$, then we're still okay.

More to the point, the purpose of this exercise is not to determine the electric and magnetic fields to high orders of $u/c$, but rather to lend physical intuition to the way in which electric and magnetic fields evolve self-consistently with one another. Students (and former students :) ) tend to say things like "changing electric fields produce magnetic fields" which, in a strict sense, isn't true. Neither causes the other, so much as they evolve simultaneously so as to satisfy Maxwell's equations.

Often times, instructors start from Maxwell's equations, derive the wave equations for the electric and magnetic fields (or potentials), and then use them to calculate things like this. Feynman takes a more "ground-level" approach, and uses Maxwell's equations directly (along with some physical insights) to produce the correct answer. The problem itself is a bit artificial, but it works just fine for its intended purpose, and it's a refreshing way to build intuition.

Answer 2

---

The first part of my question was satisfactorily addressed by J. Murray.

The remaining part is really a follow-on to my previous question. That question might be reworded as: How does Feynman get the result that $E_y\ne{0}$ is constant between the source plane and the wave-front?

The answer is that, since the source is an infinite plane, the source and wave-front form a closed boundary because they share a common boundary "at infinity". For any boundary spanning the wave-front like that shown in figure 18.6 the The time rate of change of magnetic flux through the bounded surface will only depend on the length of $L$. Were the source finite in extent, the wave front would expand in all direction. The magnitude of magnetic field variation at any point along the wave-front would therefore decrease with distance from the radiator.

But that answer begs the question of what source is responsible for the presence of the constant $E_y$ between the source and the wave-front? The answer is that the contribution from an annulus lying in the source plane and centered on the perpendicular line segment between the source and a field point where the field is to be measured is independent of the radius of the annulus. The transition period during which the conducting sheet accelerates is the only time an electric field is generated. That is because it is the only time when there is a changing magnetic field. As the event horizon of the transition period expands along the source plane, the annulus thereby determined contributes the same $E_y$ at all times.

Answer 3

Feynman's sheet had infinite extent, and it was set to motion during zero time. Is that possible? Yes, if the sheet stretches so that there is no length contraction.

In that case there still exists an electric field in all frames except for the original frame, because in all other frames except the original rest-frame the sheet contracts or extends - during a time that is non-zero.

There is a magnetic field in the original rest-frame, because a current loop (a compass) that is at rest in that frame contains moving charges, which observe a charge density that has changed from the original charge density.

And a test charge will feel an induced electric field when the charges on the sheet accelerate, because the test charge's idea about where the accelerating charges are is affected by the finite speed of information transfer.

I mean, if accelerations of charges appear to be direction-dependent then apparent changes of charge densities will be observed by the test charge during the acceleration. And as apparent speed of approach can be super-luminal, while apparent receding speed can not be super-luminal, we can see that the apparent accelerations must be direction dependent.