1

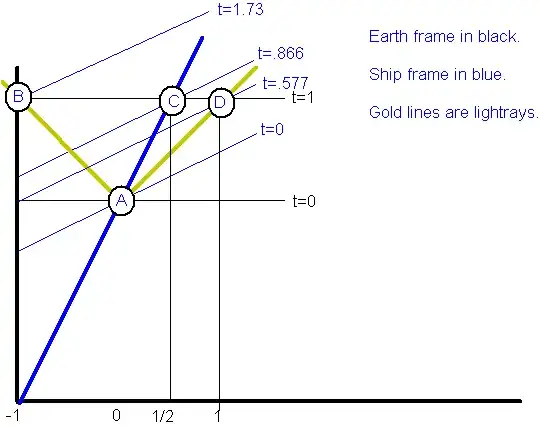
If the spaceship, travelling at c/2 were to turn on only its forward facing headlights, then after one second (relative to us, the stationary external observers) we would see that the ship has moved half a light second, whereas the first photon to be emitted from the headlight one entire light second. Relative to the crew, however, the photon would have travelled only half a light second. Therefore, Special Relativity jumps in to explain that the crew would have only experienced half a second of time since the headlights were turned on. This means that only after another second (for us) passes, will the photon have travelled one light second relative of the ship, and the crew would measure one second of elapsed time. So, for every second that passes for the crew, two have passed for us. Here's where this breaks apart for me:

What if the crew we're to turn on their headlights in the opposite direction of the ship's motion? What I imagine would happen is that, since the speed of light is always the same, then after one second (for us), the first photon to come off of the back of the ship will have travelled one light second "backwards", whereas the ship half a light second forwards, so that the total distance between them is 1.5 light seconds. The issue is that during our one second, as explained above, the crew will have measured only half a second of elapsed time. Yet, if them look back, they will see how during that half second those photons will have travelled 1.5 light seconds! This would mean that after one second, the crew will see that the photon has travelled 3 light seconds.

If my question is not understandable, I can throw in a sketch.

Izak the coder
  • 17

1 Answers1

4

If you'd thrown in the right sketch, you could have simply read off the answer:

enter image description here

According to the earth observer, there are stationary mileposts every light-second. The earth is at milepost $-1$, and the ship is at milepost $0$ when it emits its light beams going forward and backward (A). At time $1$, the backward beam reaches earth (B), the ship reaches milepost $1/2$ (C), and the forward light beam reaches milepost $1$ (D).

According to the ship observer, the same mileposts are located .866 light-seconds apart, and are traveling "backward" (i.e. toward where the earth is right now) at speed $1/2$. When I release the lightbeams (A), milepost $1$ is .866 light-seconds away, and traveling toward me at speed $1/2$, while the forward light beam travels toward it at speed $1$. They meet up (D) at time $.577$ and location $.577$. Meanwhile, milepost $1/2$ has been moving toward me at speed $1/2$, and it catches up with me at time $.866$ (C). Finally, the earth has been moving away from me at speed $1/2$ while the backward lightbeam has been chasing it at speed $1$; the lightbeam catches up with it (B) at time $1.73$ and location $-1.73$.

WillO
  • 18,387