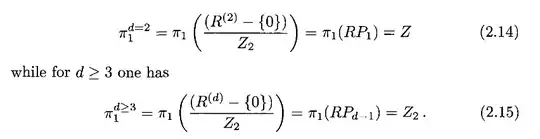In Khare's book of fractional statistics and quantum theory, when discussing why we need fractional statistics he arrives at the configuration space
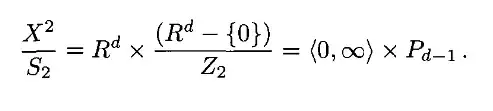
for a system of two identical particles in $d$ spatial dimensions.
Q1: I do not see how the second equality is justified. ($P_{d-1}$ is the $d-1$ dimensional real projective space, and $\langle 0,\infty \rangle$=$(0,\infty)-\{0\}$).
Q2: He seems to imply that $(\mathbb R^2 - \{0\})/\mathbb Z_2 = \mathbb R P_{1}$. But actually $\mathbb R P_{1} = (\mathbb R^2 - \{0\})/\sim $ with $x\sim y$ iff they lie on the same line. Maybe there is a physical reason to make this identification $(\mathbb R^2 - \{0\})/\mathbb Z_2 = \mathbb R P_{1}$?