Let's do a quick thought experiment to see why the speed does not affect the gravitational force between the masses. I'm going to modify your experiment slightly. We'll put a clock on each mass, and we'll start with the masses in contact. We'll give the give the two masses some initial small speed away from each other - this speed is small enough that relativistic effects can be ignored - so the masses separate, then slow to a halt then fall back together again.
Now, we're going to work in the centre of mass frame of our two masses. At the moment the masses separate we set both clocks to zero. We've started with the two masses together so that the two clocks are at the same point in spacetime, and we can therefore unambiguously synchronise both clocks to zero at the same time. All observers will agree that at the moment of separation the two clocks read zero.
The masses move away from each other until their mutual gravitational fields bring them to a halt, then they move towards each other and collide again at time $T$. That is at the moment of collision both clocks show the time to be $T$. Again both clocks are back in the same place so they can be directly compared. Again all observers will agree that the clocks show time $T$ at the moment of collision. So overall the process looks like this:
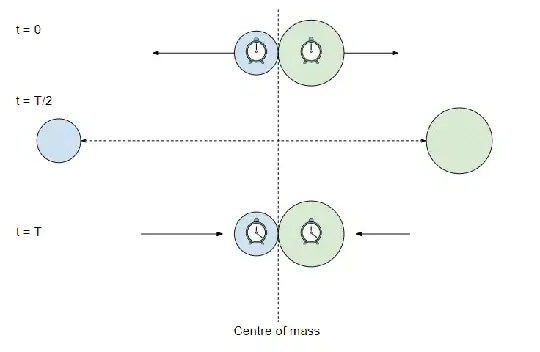
But now suppose that you're in a rocket zooming past our experiment at $0.999c$. There will be various time dilation effects associated with your motion, but you are still going to agree that the two clocks showed $t=0$ when the masses separated and $t=T$ when they collided again. So you're going to agree that in the COM frame of the masses the process took $T$ seconds.
But all velocities are relative. Having the masses stationary and you zooming past at $0.999c$ is the same as having you stationary and the masses moving past you at $0.999c$. But that means with the masses moving past you at $0.999c$ they still separate when the clocks say zero and recollide when the clocks say $T$, and therefore even when the masses are moving at $0.999$ the process still takes $T$ seconds.
But of course the time taken for the masses to separate and recollide depends on the gravitational force, and since the time hasn't changed that means the gravitational force can't have changed either. Hence we have to conclude that having the masses move at $0.999c$, or indeed any speed, does not change the gravitational force between them.
