3

I mean, we calculate the speed of a wave (in a string) by considering the tensional force as a centripetal one (that's obviously an approximation), so shouldn't potential energy decrease in the direction where it acts? Shouldn't it be maximum at the position of maximum displacement?

Vishnu
  • 5,336
Aabesh Ghosh
  • 437

1 Answers1

4

Shouldn't it be maximum at the position of maximum displacement?

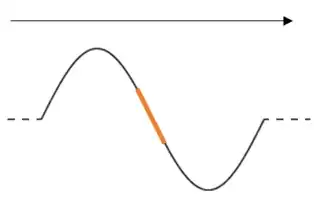
Nope, it's zero there. This system isn't the same as a mass oscillating on a spring, where potential energy is quadratic in displacement, because the tension which acts as a restoring force works differently: the string has a high elastic potential energy when it's stretched, and that stretching happens wherever you have a large slope, like the orange area:

enter image description here

If we consider a travelling wave $y(x, t)=A\sin(kx-\omega t)$, where $y$ is the displacement and $x$ is the distance between the end of the string and a given point, the tension is maximum wherever $\frac{\mathrm{d}y}{\mathrm{d}x}$ is maximum. That's clearly at the mean position.

The kinetic energy is also at a maximum at mean positions, so unlike the case of SHM, the kinetic energy and potential energy are in the same phase. The total kinetic and potential energy across the whole string is the same at any time, but the total energy at a point $x$ varies over time.