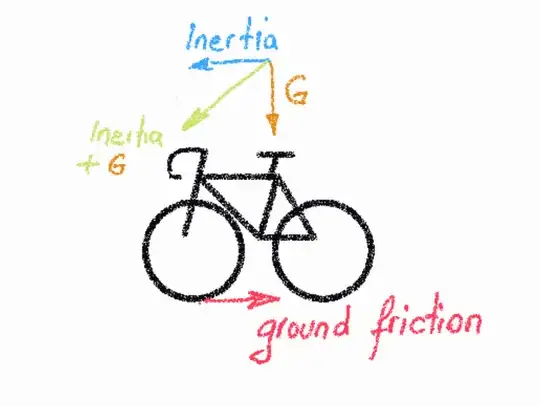
The brief answer to this is 'because the centre of mass of a bicycle is high up', and especially it is high up compared to a car, where often the front wheels can slip.
To see how this works, consider a vastly oversimplified model of a bike: assume that the structure of the bike is light compared to its rider, and represent its rider as a point mass (see below for why this works even when that's not true). And we're going to be interested in the moment when the rear wheel lifts, so we can completely ignore the rear wheel, and concentrate just on the front wheel, and specifically on the point at which the front wheel touches the road. So the system looks something like this:

So, here, $c$ is the point at which the front tyre is touching the road, $m$ is the rider, and the horizontal & vertical distances between $c$ and $m$ are $l$ & $h$ respectively. And the bike is decelerating at $a$. And I've drawn the forces exerted by the front wheel on the road at $c$ (remember the back wheel is, by assumption, just lifting, so can be ignored: it's not exerting any forces on anything).
For now assume that the coefficient of friction between the front wheel and the road is sufficiently high that the wheel does not slip and lets work out the point at which the bike just begins to tumble over the front wheel: this will tell us the maximum possible value of $a$, however sticky the front wheel is.
It's pretty easy to see that the force on $m$ has two components: a vertical component which is $-mg$, where $g$ is acceleration due to gravity, and a horizontal component which is $ma$, where $a$ is the horizontal acceleration. And the bike will tumble when this vector points above the front wheel. Well, just by drawing the appropriate components you can see that this is true when
$$\frac{ma}{mg} \gt \frac{l}{h}$$
or in other words, for the bike not to tumble
$$a \le \frac{lg}{h}$$
or
$$a_\text{max} = \frac{lg}{h} \tag{1}$$
You can convince yourself this is right: a very tall bike ($h \gg l$) will tumble really easily, and a completely flat bike ($h \ll l$) will almost never tumble. And a bike in very low gravity will tumble more easily than one in high gravity. So (1) tells us how big $a$ can be, however sticky the front wheel is.
Now consider the coefficient of friction at the front wheel. The coefficient of friction, $\mu$ is defined as the force with which the wheel is trying to slide along the road and the force which it is being pressed down onto the road, at the point where the wheel just slips. So it's obvious that,
$$\mu = \frac{ma_\text{slip}}{mg} = \frac{a_\text{slip}}{g}$$
where $a_\text{slip}$ is the point at which the wheel slips. In other words
$$a_\text{slip} = \mu g \tag{2}$$
And now we can use (1) & (2) to give us the answer we're looking for: the bike will tumble before it drifts if $a_\text{slip} \gt a_\text{max}$, in other words if
$$\mu \gt \frac{l}{h}$$
And you can now see the problem here: bikes are rather short and rather tall, so $l/h$ tends to be rather small, which means that the bike will tumble over the front wheel with a lower critical value of $\mu$. And modern tyres on dry roads have values of $\mu$ which can be fairly close to $1$ (I think $0.8$ to $0.9$ is plausible), while $l/h$ is generally significantly less than $1$.
This is why bikes tumble before they drift.
This approximation can be used even if the bike (or other vehicle) isn't light compared to the rider: you just need to work out where the centre of mass of the vehicle is and use that. For vehicles with suspension (some bikes have this of course, and even for bikes that don't the forks deflect under braking) you have to take into account the change in geometry under braking as well.