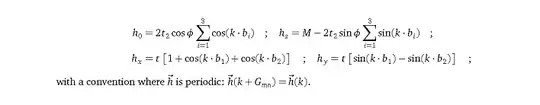Many Hamiltonians in 2D quantum systems can be parameterized as a surface (such as the Bloch sphere) by their k-space coordinates. Another example is given by the (kx,ky) points of the Brillouin torus in the 2D Haldane model that allow us to parameterize a surface based off the following Hamiltonian:
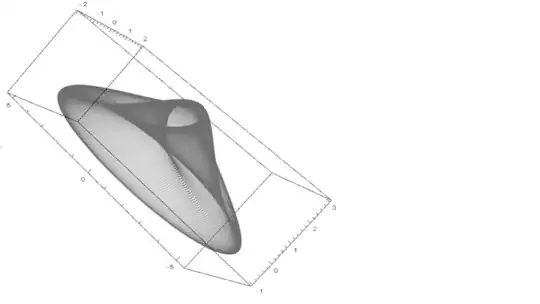
to give one a surface like this:
My question is: what do the geodesics of this surface correspond to?
According to Wikipedia,
In the presence of an affine connection, a geodesic is defined to be a curve whose tangent vectors remain parallel if they are transported along it. If this connection is the Levi-Civita connection induced by a Riemannian metric, then the geodesics are (locally) the shortest path between points in the space.
However, what does a geodesic correspond to in condensed matter systems? My intuition is these curves correspond to paths that would result in non-changing Berry phase. However, I am confused as to how this ties to the local magnetic flux. Should the flux be zero along these geodesics? Does it even make sense to think about geodesics on a 'Hamiltonian surface' (or are they useful)? Does it somehow highlight anything important about the energy (maybe since the Berry phase is unchanged, we are more likely to expect particles to take these geodesic paths in an adiabatically evolving system, as opposed to paths that are not geodesics)?
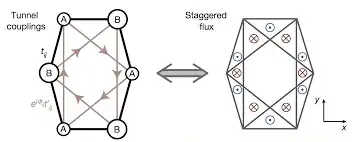
To clarify what I mean by 'local magnetic flux', let me exemplify using Haldane's model: to the right of the image below (source), we see that the model results in magnetic flux pointing in different directions (in vs out). Do geodesics correspond to lines that separate regions of in/out? Are we guaranteed that the flux = 0 (regardless of continuity)?
There are several posts on this website about the geodesics of Hamiltonians in the context of general relativity (such as Finding geodesics: Lagrangian vs Hamiltonian), but I was not able to find good resources that discuss geodesics in the context of my post. Therefore, I would appreciate any advice or resource recommendations. Thank you!