Retarded potentials with a dirac delta fail to give Lienard-Wiechert

Question

In the derivation of the Liénard-Wiechert potential the expression for the retarded potential is given $$\varphi(\mathbf{r}, t) = \frac{1}{4\pi \epsilon_0}\int \frac{\rho(\mathbf{r}', t_r')}{|\mathbf{r} - \mathbf{r}'|} d^3\mathbf{r}'$$

and it is applied to a moving particle, given by the time varying distribution (a moving dirac delta):

$$\rho(\mathbf{r}', t') = q \delta^3(\mathbf{r'} - \mathbf{r}_s(t'))$$

Now why is it NOT the case that for this particular time-varying distribution we simply have:

$$\varphi(\mathbf{r}, t) = \frac{1}{4\pi \epsilon_0} \frac{q}{|\mathbf{r} - \mathbf{r}_s (t')| } $$

?

i.e., why does it not directly follow form the definition of the Dirac delta given by:

$$\int f(x) \delta(x - x_0) = f(x_0)$$

?

Being a mathematician familiar with distributions in the sense of Schwartz, I would like a mathematically rigorous answer in terms of this.

Answer 1

The definition of the Dirac function cannot be applied directly to obtain your third expression, because $t_r'$ in $\delta^3(\mathbf r' - \mathbf r_s(t_r'))$ is a function of $\mathbf r'$.

To evaluate the integral, one must change the integral to new integration variables $\mathbf y$ in such a way that the definition can be applied, which requires that the argument is of the form

$$ \mathbf y - \mathbf y_0 $$ where $\mathbf y_0$ does not depend on $\mathbf y$.

For example, we can introduce new variables in this way:

$$ \mathbf y = \mathbf r' - \mathbf r_s(t_r') $$

and then use this definition to reexpress the integral. In doing so a Jacobi factor will be introduced and that's why the result (Lienard-Wiechert electric potential) is different from your third expression.

Some examples of how the change of variables is done can be seen here: http://booksite.academicpress.com/andrilli/elementary/content/jacobian.pdf

Answer 2

This interesting point is treated carefully in standard textbooks such as Jackson, and the Feynman lectures present a thorough discussion of this very issue. However, I find Jackson's treatment a little formal, so that I want a further insight into what is going on, and Feynman's treatment is insightful but a bit long-winded. Therefore I developed my own derivation which can be found at figure 8.9 in my undergraduate textbook on relativity (Oxford University Press), and which I repeat here.

The way to understand this is to avoid the use of the Dirac delta function in the first instance, and treat the source event not as a point-like event but as a charge distribution of small length, with the backwards light cone form the field event extending through it.

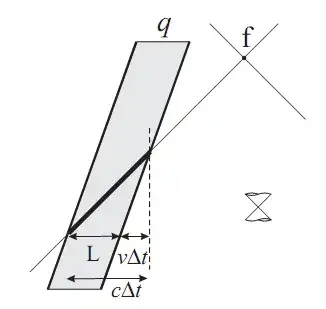
Here f marks a field event and the light cone is drawn through it. We must allow the source particle a finite spatial extent and take the limit as this becomes small compared to all other distances. The shaded region is the worldsheet of this source. The diagonal lines show the past light cone of f. The events contributing to the integral are those shown bold. Suppose we want to calculate the scalar potential $\phi$ in the reference frame whose lines of simultaneity are horizontal in the diagram. Then the (spatial) length of the contributing line of events is $s = c \Delta t$ where $\Delta t$ is the time taken for a light pulse to travel $s = L + v \Delta t$ while the lump of charge travels $v \Delta t$, where $L$ is equal to the length of the lump. Eliminating $\Delta t$ we find $s = L/(1-v/c)$. Thus the moving charge contributes as much to the integral as a non-moving charge of the same density but longer length would contribute. Thus when we integrate the expression for the potential, with the integral being over the volume element $dx dy dz$, the result is a factor $1/(1-v/c)$ larger than a naive (i.e. wrong) treatment would suggest, where $v$ is the component of velocity towards the field point. The naive argument goes wrong because it fails to account correctly for the time-dependent nature of the integrand. This time-dependence amounts to making the integral not so much over a time slice (hypersurface of simultaneous events) as over a light cone surface.

The above is equivalent to the use of a change of variable and a Jacobean (see reference provided by answer of Ján Lalinský). But alongside the mathematical rigour, which can equally well be obtained by such methods, I hope it also adds a physical insight into what is going on.