Question about the true nature of the Spinor mathematical object

Question

My question is kind of a silly one,but,I really would like to know what truly is a Spinor. I will explain what is my concept of "truly". Throught all the question post, consider finite vector spaces only, and $\mathbb{K} \equiv \mathbb{R}$, the field. I'm not going to exibit proofs of any kind for any object defined and exposed here. I will deal with second order tensors only,for the sake of simplicity.

1)What truly are vectors and covectors?

A vector is an mathematical object that is a member of a particular algebric structure called Vector space. That is:

$$\mathfrak {V} \equiv [\mathcal{V},(\mathbb{K},+_{\mathbb{K}},\cdot_{\mathbb{K}}),\boxplus_{\mathfrak{V}},\boxdot_{\mathfrak{V}}]$$

Where $\mathcal{V}$ is a non empty set of elements, $(\mathbb{K},+_{\mathbb{K}},\cdot_{\mathbb{K}})$ another algebric structure called a Field; $\boxplus_{\mathfrak{V}}$ and $\boxdot_{\mathfrak{V}}$ are two binary operations called, respectively, sum of vectors and scalar multiplication.

The sum of vectors is defined as:

$$\begin{array}{rl} \boxplus_{\mathfrak{V}} :\mathcal{V}\times \mathcal{V} &\to \mathcal{V} \\ (v,u)&\mapsto \boxplus_{\mathfrak{V}}(v,u) \equiv v \boxplus_{\mathfrak{V}} u \end{array}$$

The scalar multiplication is defined as:

$$\begin{array}{rl} \boxdot_{\mathfrak{V}} :\mathbb{K}\times \mathcal{V} &\to \mathcal{V} \\ (\alpha,v)&\mapsto \boxdot_{\mathfrak{V}}(\alpha,v)\equiv \alpha \boxdot_{\mathfrak{V}} u \end{array}$$

Evenmore, each one of them must to satisfy some properties:

For $\boxplus_{\mathfrak{V}}$:

(Associativity): $v \boxplus_{\mathfrak{V}} (u\boxplus_{\mathfrak{V}} w) = (v\boxplus_{\mathfrak{V}} u)\boxplus_{\mathfrak{V}} w$

(Comutativity): $ v \boxplus_{\mathfrak{V}} u = u\boxplus_{\mathfrak{V}} v$

(Existence of Neutral Element): $\forall v\in \mathcal{V},$ $\exists $ $0_{\mathfrak{V}} $ $|$ $ v\boxplus_{\mathfrak{V}} 0_{\mathfrak{V}} = v = 0_{\mathfrak{V}}\boxplus_{\mathfrak{V}} v$

(Existence of opposite Element): $\exists (-v)$, for each,$v\in \mathcal{V},$ $|$ $ v\boxplus_{\mathfrak{V}} (-v) = 0_{\mathfrak{V}} = (-v) \boxplus_{\mathfrak{V}} v$

For $\boxdot_{\mathfrak{V}}$:

$\alpha \boxdot_{\mathfrak{V}} (v\boxplus_{\mathfrak{V}} u) = \alpha \boxdot_{\mathfrak{V}} v \boxplus_{\mathfrak{V}} \alpha \boxdot_{\mathfrak{V}}u$

$ (\alpha +_{\mathbb{K}} \beta)\boxdot_{\mathfrak{V}} v = \alpha \boxdot_{\mathfrak{V}} v \boxplus_{\mathfrak{V}} \beta \boxdot_{\mathfrak{V}}v $

$ (\alpha \cdot_{\mathbb{K}} \beta)\boxdot_{\mathfrak{V}} v = \alpha \boxdot_{\mathfrak{V}} (\beta \boxdot_{\mathfrak{V}}v)$

$1_{\mathbb{K}} \boxdot_{\mathfrak{V}} v = v$

Where $1_{\mathbb{K}}$ is the identity element, or the unit scalar from the field (in our case $1_{\mathbb{K}} = 1\in \mathbb{R}$, and $0_{\mathfrak{V}}$ is the zero vector of the vector space.

So, with all these properties we can speak truly (we defined whats is) about what is a vector.

$$ * * *$$

Consider now, a new kind of object which generalizes the notion of a linear function; the new objects are called Linear Transformations (or linear maps):

$$\begin{array}{rl} L :\mathfrak{V} &\to \mathfrak{W} \\ v&\mapsto L[v] := \cdot\end{array}$$

(the symbol $L[v]$ means both that the linear map L is acting on a vector v and, the image of L in $\mathfrak{W}$). The other symbol $:= \cdot$ means "give some definition for $L$")

And these Linear maps, must satisfy two "constrains" called linearity condition:

$L[v \boxplus_{\mathfrak{V}} u ] = L[v] \boxplus_{\mathfrak{W}} L[u]$

$L[\alpha \boxdot_{\mathfrak{V}} v] = \alpha \boxdot_{\mathfrak{W}} L[v]$

Now, consider then the set of all linear maps:

$$\mathcal{L}(\mathfrak{V},\mathfrak{W})\equiv \mathcal{L} = \Big\{ L\in \mathcal{L}(\mathfrak{V},\mathfrak{W}) | L: \mathfrak{V} \to \mathfrak{W} \Big\}$$

and then define two new binary operations:

$$\begin{array}{rl} \boxplus_{\mathfrak{Lin}} :\mathcal{L}\times \mathcal{L} &\to \mathcal{L} \\ (L,T)&\mapsto \boxplus_{\mathfrak{Lin}}(L,T) \equiv L \boxplus_{\mathfrak{Lin}} T \end{array}$$

$$\begin{array}{rl} \boxdot_{\mathfrak{Lin}} :\mathbb{K}\times \mathcal{L} &\to \mathcal{L} \\ (\alpha,L)&\mapsto \boxdot_{\mathfrak{Lin}}(\alpha,L) \equiv \alpha \boxdot_{\mathfrak{Lin}} L \end{array}$$

Now, these operations acctually defines two maps,called:

The sum of linear maps, defined as:

$$\begin{array}{rl} L \boxplus_{\mathfrak{Lin}} T:\mathfrak{V} &\to \mathfrak{W} \\ v&\mapsto (L \boxplus_{\mathfrak{Lin}} T)[v] := L[v] \boxplus_{\mathfrak{W}} T[v] \end{array}$$

The scalar multiplication of linear maps, defined as:

$$\begin{array}{rl} \alpha \boxdot_{\mathfrak{Lin}} L:\mathfrak{V} &\to \mathfrak{W} \\ v&\mapsto (\alpha \boxdot_{\mathfrak{Lin}} L)[v] := \alpha \boxdot_{\mathfrak{W}} L[v] \end{array}$$

and each one must satisfy the linearity condition to become a linear map.

Then,with the machinery above we can call the set $\mathcal{L}(\mathfrak{V},\mathfrak{W})$ a vector space.

$$ \mathfrak{Lin}(\mathfrak{V},\mathfrak{W}) \equiv \mathfrak{Lin} \equiv [\mathcal{L}(\mathfrak{V},\mathfrak{W}),(\mathbb{K},+_{\mathbb{K}},\cdot_{\mathbb{K}}),\boxplus_{\mathfrak{Lin}},\boxdot_{\mathfrak{Lin}}]$$

This vector space is called Vector Space of Linear Transformations. And the elements are called (obviously) Linear Transformations or Linear Maps

$$ * * *$$

Consider now a particular kind of linear map defined as:

$$\begin{array}{rl} f:\mathfrak{V} &\to \mathbb{K} \\ v&\mapsto f[v] := \cdot\end{array}$$

and then consider the set of all these linear maps:

$$\mathcal{L'}(\mathfrak{V},\mathbb{K}) = \mathcal{L'} = \Big\{ f \in \mathcal{L}(\mathfrak{V},\mathbb{K}) | f: \mathfrak{V} \to \mathbb{K} \Big\}$$

and then define two binary operations:

$$\begin{array}{rl} \boxplus_{\mathfrak{Lin}'} :\mathcal{L'}\times \mathcal{L'} &\to \mathcal{L'} \\ (f,g)&\mapsto \boxplus _{\mathfrak{Lin}'}(f,g) \equiv f \boxplus_{\mathfrak{Lin}'} g \end{array}$$

$$\begin{array}{rl} \boxdot_{\mathfrak{Lin}'} :\mathbb{K}\times \mathcal{L'} &\to \mathcal{L'} \\ (\alpha,f)&\mapsto \boxdot_{\mathfrak{Lin}'}(\alpha,f) \equiv \alpha \boxdot _{\mathfrak{Lin}'} f \end{array}$$

Now, these operations acctually defines two maps,called:

The sum of covectors, defined as:

$$\begin{array}{rl} f \boxplus_{\mathfrak{Lin}'} g:\mathfrak{V} &\to \mathbb{K} \\ v&\mapsto (f \boxplus_{\mathfrak{Lin}'} g)[v] := f[v] + _{\mathbb{K}} g[v] \end{array}$$

The scalar multiplication of covectors, defined as:

$$\begin{array}{rl} \alpha \boxdot_{\mathfrak{Lin}'} f:\mathfrak{V} &\to \mathbb{K} \\ v&\mapsto (\alpha \boxplus_{\mathfrak{Lin}'} f)[v] := \alpha \cdot_{\mathbb{K}}f[v] \end{array}$$

and,again, each one must satisfy the linearity condition to become a linear map.

Then,with the machinery above we can call the set $\mathcal{L}(\mathfrak{V},\mathbb{K})$ a vector space.

$$ \mathfrak{Lin}'(\mathfrak{V},\mathbb{K}) \equiv \mathfrak{V}^{*} \equiv [\mathcal{L}(\mathfrak{V},\mathbb{K}),(\mathbb{K},+_{\mathbb{K}},\cdot_{\mathbb{K}}),\boxplus_{\mathfrak{Lin}'},\boxdot_{\mathfrak{Lin}'}]$$

This vector space is called Dual Vector Space. The elements of the dual vector space are called Covectors

$$ * * *$$

So, we have defined what is a vector, a linear map and a covector. In particular for vectors and covectors, there is a mathematical fact (concerning the basis of a vector space and dual space) which allows us to write an element of $\mathfrak{V}$ (and $\mathfrak{V}^{*}$) in terms of a linear combination of other vectors, called basis vectors $\vec{e}_{\mu}$ and basis covectors $e'^{\nu}$:

For vectors (also called Contravariant Vectors) we have:

$$ \vec{v} = \sum _{\mu}v^{\mu} \boxdot _{\mathfrak{V}} \vec{e}_{\mu}$$

For a covectors (also called,Linear Functional, Convariant Vectors and Linear Form) we have:

$$ f'[v]= (\sum _{\nu}f_{\nu} \boxdot _{\mathfrak{V}} e'^{\nu})[v] \implies f= \sum _{\nu}f_{\nu} \boxdot _{\mathfrak{V}} e'^{\nu}$$

$$ * * *$$

2)What truly is a tensor?

It's quite commom to define tensors as objects that have a quite predictible behavior called transformation of components with respect to two coodinates; $x^{\gamma} \to x'^{\gamma}(x^{\gamma}) $:

$$T'^{\mu}_{\nu} = \frac{\partial x'^{\mu}}{\partial x^{i}} \frac{\partial x^{j}}{\partial x'^{\nu}}T^{i}_{j} $$

where the $T'^{\mu}_{\nu} $ are the components of the Tensor T in coordinates $x'^{\gamma}(x^{\gamma})$ and, similarly $T^{i}_{j} $ are the components of the same tensor $T$ in coordinates $x^{\gamma}$. And the forest of partials are acctually what means "predictible behavior"; they are jacobian matrices or, coordinate transformation matrices.

So, ok, we have this definition of a tensor. But what does it mean "Tensor T" ? Well, to answer this question, we have to exibit the tensor as

$$T =T^{\mu}_{\nu}\boxdot (some "tensor" basis)$$

and some sort of "tensor space".

The truth is, both of these concepts are well defined.

$$* * *$$

The true answer for the question "what is a tensor?" is that the mathematical object called Tensor, is merely an element of a algebric structure called Tensor Product vector space (or just Tensor product or Tensor Space).

But in order to talk about tensors we need a little (necessary) digression on bilinearity.

2.1) Bilinear Maps

It's well know from elementary linear algebra the notion of inner product. And even before linear algebra, in vector calculus you certainy studied the scalar product $\vec{A} \cdot \vec{B}$. But,again, from elementary linear algebra you realized that the scalar product is just a particular example of inner product. But the core of the operation is that the whole process deals with two vectors (to return a scalar in this case).

In general we have then that the inner product is defined as the following map:

$$\begin{array}{rl} \langle \cdot ,\cdot \rangle :\mathfrak{V}\times \mathfrak{W} &\to \mathbb{K} \equiv \mathfrak{Z} \\ (v,w)&\mapsto \langle \cdot ,\cdot \rangle[(v,w)] \equiv \langle v ,w \rangle :=\cdot \end{array}$$

and, the inner product must satisfy the following properties:

$1) \langle v \boxplus _{\frak V} v' ,w \rangle = \langle v ,w \rangle \boxplus _{\mathbb{K}} \langle v' ,w \rangle$

$2) \langle v,w \boxplus _{\frak W} w' \rangle = \langle v ,w \rangle \boxplus _{\mathbb{K}} \langle v ,w' \rangle$

$3) \langle \alpha \boxdot _{\frak V} v , w \rangle = \alpha \boxdot _{\mathbb{K}} \langle v ,w \rangle $

$4) \langle v , \alpha \boxdot _{\frak W} w \rangle = \alpha \boxdot _{\mathbb{K} } \langle v ,w \rangle $

$5) \langle v ,w \rangle = \langle w ,v \rangle$

$6) \langle v ,v \rangle \geq 0_{\mathbb{K}} $

$7)$ If $\langle v ,v \rangle = 0_{\mathbb{K}} \implies v = 0_{\mathfrak{V}}$

Well, this particular map shows to us, with properties $1)$ to $4)$ the bilinear nature of a map, which means that the whole map is linear on each slot. In other words, each slot defines a linear map.

$$\begin{array}{rl} \langle \_,\cdot \rangle :\mathfrak{V}&\to \mathbb{K} \equiv \mathfrak{Z} \\ v&\mapsto \langle \_,\cdot \rangle[v] \equiv \langle v ,\cdot \rangle :=\cdot \end{array}$$

$$\begin{array}{rl} \langle \cdot,\_ \rangle :\mathfrak{W}&\to \mathbb{K} \equiv \mathfrak{Z} \\ w&\mapsto \langle \cdot,\_ \rangle[w] \equiv \langle \cdot, w \rangle :=\cdot \end{array}$$

$$ * * *$$

So now, we can define a new kind of object called Bilinear Transformation (or bilinear map, bilinear function) as:

$$\begin{array}{rl} B:\mathfrak{V}\times \mathfrak{W} &\to \mathfrak{X} \\ (v,w)&\mapsto B[(v,w)] :=\cdot \end{array}$$

and, the bilinear map must satisfy the following properties:

$1) B[(v \boxplus _{\frak V} v' ,w)] = B[(v ,w)] \rangle \boxplus _{\frak{X}} B(v' ,w)]$

$2) B[(v,w \boxplus _{\frak W} w')] = B[(v ,w)] \boxplus _{\frak{X}} B[(v ,w')]$

$3) B[(\alpha \boxdot _{\frak V} v , w)] = \alpha \boxdot _{\frak X}B[(v , w)] $

$4) B[(v,\alpha \boxdot _{\frak W} w)] = \alpha \boxdot _{\frak X}B[(v , w)] $

Now, consider then the set of all bilinear maps:

$$\mathcal{L}_{2}(\mathfrak{V}\times\mathfrak{W};\mathfrak{X})\equiv \mathcal{L}_{2} = \Big\{ B\in \mathcal{L}_{2}(\mathfrak{V}\times\mathfrak{W},\mathfrak{X}) | B: \mathfrak{V} \times \mathfrak{W} \to \mathfrak{X} \Big\}$$

and then define two new binary operations:

$$\begin{array}{rl} \boxplus_{\mathfrak{Lin}_{2}} :\mathcal{L}_{2}\times \mathcal{L}_{2} &\to \mathcal{L}_{2} \\ (B,M)&\mapsto \boxplus_{\mathfrak{Lin_{2}}}(B,M) \equiv B \boxplus_{\mathfrak{Lin_2}} M \end{array}$$

$$\begin{array}{rl} \boxdot_{\mathfrak{Lin}_{2}} :\mathbb{K}\times \mathcal{L}_{2} &\to \mathcal{L}_{2} \\ (\alpha,B)&\mapsto \boxdot_{\mathfrak{Lin_{2}}}(\alpha,B) \equiv \alpha \boxplus_{\mathfrak{Lin_2}} B \end{array}$$

Now, these operations acctually defines two maps,called:

The sum of bilinear maps, defined as:

$$\begin{array}{rl} B \boxplus_{\mathfrak{Lin_{2}}} M:\mathfrak{V}\times \mathfrak{W} &\to \mathfrak{X} \\ (v,w)&\mapsto (B \boxplus_{\mathfrak{Lin_{2}}} M)[(v,w)] := B[(v,w)] \boxplus_{\mathfrak{X}} M[(v,w)] \end{array}$$

The scalar multiplication of bilinear maps, defined as:

$$\begin{array}{rl} \alpha \boxdot_{\mathfrak{Lin_{2}}} B:\mathfrak{V} \times \mathfrak{W} &\to \mathfrak{X} \\ (v,w)&\mapsto (\alpha \boxdot_{\mathfrak{Lin_{2}}} B)[(v,w)] := \alpha \boxdot_{\mathfrak{X}} B[(v,w)] \end{array}$$

and each one must satisfy the bilinearity conditions to become a bilinear map.

Then,with the machinery above we can call the set $\mathcal{L}_{2}(\mathfrak{V},\mathfrak{W},\mathfrak{X})$ a vector space.

$$ \mathfrak{Lin_{2}}(\mathfrak{V},\mathfrak{W};\mathfrak{X}) \equiv \mathfrak{Lin_{2}} \equiv [\mathcal{L}_{2}(\mathfrak{V},\mathfrak{W};\mathfrak{X}),(\mathbb{K},+_{\mathbb{K}},\cdot_{\mathbb{K}}),\boxplus_{\mathfrak{Lin_{2}}},\boxdot_{\mathfrak{Lin_{2}}}]$$

This vector space is called Vector Space of Bilinear Transformations. And the elements are called (obviously) Bilinear Transformations or Bilinear Maps

$$* * *$$

Consider now a particular kind of bilinear map defined as:

$$\begin{array}{rl} b:\mathfrak{V}\times \mathfrak{V} &\to \mathbb{K} \\ (v,w)&\mapsto b[(v,w)] := \cdot\end{array}$$

and then consider the set of all these bilinear maps:

$$\mathcal{L'}_{2}(\mathfrak{V}\times\mathfrak{V};\mathbb{K}) = \mathcal{L'}_{2} = \Big\{ b \in \mathcal{L'}_{2}(\mathfrak{V}\times\mathfrak{V},\mathbb{K}) | b: \mathfrak{V}\times \frak V \to \mathbb{K} \Big\}$$

and then define two new binary operations:

$$\begin{array}{rl} \boxplus_{\mathfrak{Lin'}_{2}} :\mathcal{L'}_{2}\times \mathcal{L'}_{2} &\to \mathcal{L'}_{2} \\ (B,M)&\mapsto \boxplus_{\mathfrak{Lin_{2}}}(B,M) \equiv B \boxplus_{\mathfrak{Lin'_2}} M \end{array}$$

$$\begin{array}{rl} \boxdot_{\mathfrak{Lin'}_{2}} :\mathbb{K}\times \mathcal{L'}_{2} &\to \mathcal{L'}_{2} \\ (\alpha,B)&\mapsto \boxdot_{\mathfrak{Lin'_{2}}}(\alpha,B) \equiv \alpha \boxplus_{\mathfrak{Lin'_2}} B \end{array}$$

Now, these operations acctually defines two maps,called:

The sum of bilinear forms, defined as:

$$\begin{array}{rl} B \boxplus_{\mathfrak{Lin'}_{2}} M:\mathfrak{V}\times \mathfrak{V} &\to \mathbb{K} \\ (v,w)&\mapsto (B \boxplus_{\mathfrak{Lin'_{2}}} M)[(v,w)] := B[(v,w)] \boxplus_{\mathfrak{K}} M[(v,w)] \end{array}$$

The scalar multiplication of bilinear forms, defined as:

$$\begin{array}{rl} \alpha \boxdot_{\mathfrak{Lin'_{2}}} B:\mathfrak{V} \times \mathfrak{V} &\to \mathbb{K} \\ (v,w)&\mapsto (\alpha \boxdot_{\mathfrak{Lin'_{2}}} B)[(v,w)] := \alpha \boxdot_{\mathbb{K}} B[(v,w)] \end{array}$$

and,again, each one must satisfy the bilinearity condition to become a bilinear map.

Then,with the machinery above we can call the set $\mathcal{L'}_{2}(\mathfrak{V},\mathfrak{V};\mathbb{K})$ a vector space.

$$ \mathfrak{Lin_{2}}'(\mathfrak{V},\mathfrak{V};\mathbb{K}) \equiv[\mathcal{L'}_{2}(\mathfrak{V},\mathbb{K}),(\mathbb{K},+_{\mathbb{K}},\cdot_{\mathbb{K}}),\boxplus_{\mathfrak{Lin}'_{2}},\boxdot_{\mathfrak{Lin}'_{2}}]$$

This vector space has no particular famous name, but the elements of this vector space are called Bilinear Forms or Bilinear Functionals.

$$ * * * $$

So, after the introduction to the concept of bilinearity and bilinear maps the path to understand the core concept of tensors are almost done.

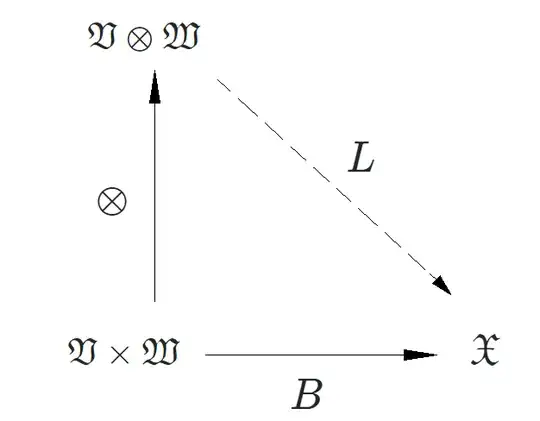
Definition: A tensor product is a pair: $(\mathfrak{T},\bar{\otimes})$. $\frak T$ is a vector space and $\otimes$ is a bilinear operation (function) which satisfies the following "constrain":

$$B = L \circ \otimes$$

which is the mathematical symbol for the comutative diagram:

Where $B$ is a bilinear map (if other sorts of particular properties), $\otimes$ is the tensor map (which is bilinear and JUST bilinear) and $L$ is a linear map.

Now, in order to ensure that this construction is valid, Steven Roman (Advanced Linear Algebra,Springer,pag 361-366) constructs $\frak V \otimes \frak W$ in terms of a quotient space:

$$\mathfrak{V}\otimes\mathfrak{W} := \frac{\mathfrak{F}_{(\mathfrak{V}\times\mathfrak{W})}}{\mathfrak{S}}$$

Where $\mathfrak{F}_{(\mathfrak{U}\times\mathfrak{V})}$ is called free vector space of $\frak{V}\times \frak{W}$, which elements are in the form: $$\sum^{N}_{i=1} r_{i}(u_{i},v_{i})$$

And $\mathfrak{S}$, a subspace of $\mathfrak{F}_{(\mathfrak{U}\times\mathfrak{V})}$ which are spanned by vectors of this form:

$$\alpha(v,w)+\beta (v',w)-(\alpha v+\beta v',w)$$

$$\alpha (v,w)+\beta (v,w')-(v,\alpha w+\beta w')$$

Then the elements of tensor products are indeed:

$$\sum^{N}_{i=1} [\alpha_{i}(v_{i},w_{i}) + \mathfrak{S} ]$$

Which are called equivalence classes. It's quite common to rewrite the equivalente classes (elements of tensor product i.e. tensors) as :

$$\sum^{N}_{i=1} [\alpha_{i}(v_{i},w_{i}) + \mathfrak{S}] = \sum^{N}_{i=1} v_{i}\otimes w_{i} $$

And,now, about the tensor map $\otimes$, Roman defines as following:

$$\begin{array}{rl} \otimes :\mathfrak{V} \times \mathfrak{W} &\to \mathfrak{V} \otimes \mathfrak{W} \\ (v,w)&\mapsto \otimes[(v,w)] := v \otimes w \equiv (v,w) + \mathfrak{S} \end{array}$$

And then we proves that the tensor map is indeed bilinear and the pair:

$$\Big(\frac{\mathfrak{F}_{(\mathfrak{V}\times\mathfrak{W})}}{\mathfrak{S}}, \otimes \Big)$$

Is the tensor product.

$$* * *$$

So, with that quotient construction, Roman shows to us that the idea of the tensor product is valid and works, which mean that the definition of this new vector space called tensor product, via the machinery (and necessity) of universal property holds quite good.

Then, if works fine to that quotient space, its just a matter to prove for other kinds os vector spaces if they obey that "universal machinery".

Because all of that, we can now introduce the concept of a tensor as a multilinear map, with to definitions (I will give the covariant definition) [Classical Mechanics with Mathematica,Romano,Birkhaüser,pag20-22; General Relativity,Wald,Chicago Press,pag 20]:

Definition 1 : A covariant two tensor or second order tensor (or (2,0)-tensor) is a bilinear form:

$$\begin{array}{rl} T :\mathfrak{V} \times \mathfrak{V} &\to \mathbb{K} \\ (v,w)&\mapsto T[(v,w)] := \cdot \end{array}$$

So, $T$ clearly is a member of $\mathfrak{Lin_{2}}'(\mathfrak{V},\mathfrak{V};\mathbb{K})$

Definition 2 : The tensor map is:

$$\begin{array}{rl} \bar{\otimes} :\mathfrak{V}^{*} \times \mathfrak{V}^{*} &\to \mathfrak{Lin_{2}}'(\mathfrak{V},\mathfrak{V};\mathbb{K}) \\ (v,w)&\mapsto \bar{\otimes}[(v,w)] \equiv f \bar{\otimes} g \end{array}$$

And the tensor map defines the tensor product operation, defined as:

$$\begin{array}{rl} f\bar{\otimes}g :\mathfrak{V}\times \mathfrak{V}&\to \mathbb{K} \\ (v,w)&\mapsto (f \bar{\otimes} g)[(v,w)] := f[v]\boxdot_{\mathbb{K}}g[w] \end{array}$$

Now, consider them a basis vectors ${e_{i}} \in \mathfrak{V}$.

We have that $T$, covariant 2-tensor, is a bilinear form.

$$T[(v,w)] = T[(v^{i}e_{i},w^{j}e_{j})] = (v^{i}\boxdot_{\mathbb{K}}w^{j})\boxdot_{\mathfrak{Lin_{2}}'}T[(e_{i},e_{j})] \equiv (v^{i}\boxdot_{\mathbb{K}}w^{j})\boxdot_{\mathfrak{Lin_{2}}'}T_{ij}=$$

$$= v^{i}w^{j}T_{ij}$$

But now, consider then, basis covectors ${f^{i}} \in \mathfrak{V}^{*}$ under the tensor map defined, acting in the same vectors $(v,w)$ :

$$(f^{i} \bar{\otimes} f^{j})[(v,w)] = f^{i}[v^{k}e_{k}]\boxdot_{\mathbb{K}}f^{j}[w^{m}e_{m}] = (v^{k}\boxdot_{\mathbb{K}}w^{m})f^{i}[e_{k}]\boxdot_{\mathbb{K}}f^{j}[e_{m}] =$$ $$ = (v^{k}\boxdot_{\mathbb{K}}w^{m})\boxdot_{\mathbb{K}}(\delta^{i}_{k}\boxdot_{\mathbb{K}}\delta^{j}_{m})\equiv v^{k}w^{m}\delta^{i}_{k}\delta^{j}_{m} = v^{i}w^{j}$$

Hence, we have properly that a $(0,2)$-tensor can be writen as:

$$\{T\}[(v,w)] = \{v^{i}w^{j}T_{ij} \}[(v,w)] = \{f^{i} \bar{\otimes} f^{j}T_{ij} \}[(v,w)] \implies $$

$$T = T_{ij} \boxdot _{\mathfrak{Lin'_{2}}} f^{i}\bar{\otimes}f^{j} \equiv$$

$$T = T_{ij}f^{i}\bar{\otimes}f^{j}$$

And after all of this awful text we can say that

i) The tensor product os covariant tensors are indeed:

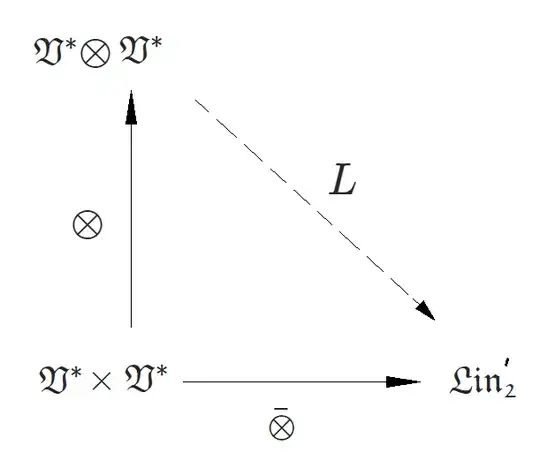
$$V^{*}\otimes V^{*}\equiv \mathfrak{T}^{0}_{2}(\mathfrak{V}) \approx [\mathfrak{Lin_{2}}'(\mathfrak{V},\mathfrak{V};\mathbb{K}),\bar{\otimes}] $$

I wrote $\approx$ not $=$ because if you look at the commutative diagram you will find that there's a linear map $L$. Well, $L$ is an isomorfism. The diagram is then:

ii) A (covariant)$(0,2)$-tensor can be written as:

$$T = \sum_{\mu}\sum_{\nu}t_{\mu \nu} e^{\mu}\bar{\otimes}e^{\nu}$$

with the particular basis vectors $e^{\mu}\bar{\otimes}e^{\nu}$ that spans the $\mathfrak{V}^{*}\otimes \mathfrak{V}^{*}$

3) What truly is a Spinor?

Well, we know what truly is a vector,a covector,a linear and bilinear maps and forms, and tensors.Truly, a vector is a member of a vector space $\mathfrak{V}$, a linear map is a member of $\mathfrak{Lin}(\mathfrak{V},\mathfrak{W})$ a covector is an element of $\mathfrak{Lin'}(\mathfrak{V},\mathbb{K})$. A bilinear map is a member of $\mathfrak{Lin}_{2}(\mathfrak{V},\mathfrak{W},\mathfrak{X})$ and a bilinear form is a member of $\mathfrak{Lin'}_{2}(\mathfrak{V},\mathfrak{W},\mathbb{K})$.

Finally, a tensor is a member of $\mathfrak{V}\otimes\mathfrak{W}$ (wherever what is the construction,here I presented two: quotient spaces and multilinear maps), a space that satisfies the universal property.

Now I would like to ask to you,what truly is a spinor? In order to answer my question please note all my text, which means that I would like an answer just in the realm of finite dimension,Fields (not rings),and vector spaces (not modules). Also,if you could, an answer friendly and intuitive but at the same time quite general and rigorous.

Answer 1

The Setup

Let $\gamma_{\mu}$ be the gamma matrices relative to the signature $(+,-,-,-)$ and let $$H(\mathbb{C}^2)= \{ A \in \mathbb{C}^{2 \times 2}| A = A^H\}$$ be the space of hermitian $2 \times 2$ matrices, a basis of which is given by the Pauli Matrices $\sigma_{\mu}, \mu =0,1,2,3$ $$ \sigma_0 = \begin{pmatrix} 1 & 0 \\ 0 & 1\end{pmatrix}, \sigma_1 = \begin{pmatrix} 0 & 1 \\ 1 & 0\end{pmatrix}, \sigma_2 = \begin{pmatrix} 0 & -i \\ i & 0\end{pmatrix}, \sigma_3 = \begin{pmatrix} 1 & 0 \\ 0 & -1\end{pmatrix}.$$ Define the isomorphisms $$f_1: \mathbb{R}^4 \to H(\mathbb{C}^2), x_{\mu}e_{\mu} \mapsto x_{\mu} \sigma_{\mu}$$ $$f_2: \mathbb{R}^4 \to H(\mathbb{C}^2), x_{\mu}e_{\mu} \mapsto x^{\mu} \sigma_{\mu} $$ where $e_{\mu}$ are the standard-basis vectors for $\mathbb{R}^4$. Using all of this, we can write the gamma matrices as $$\gamma_{\mu} = \begin{pmatrix} 0 & f_1(e_{\mu}) \\ f_2(e_{\mu}) & 0 \end{pmatrix}.$$ Finally, define the so called ''universal covering homomorphism'' $$F:SL_2\mathbb{C} \to L^{\uparrow}_+ = SO(1,3)^+$$ by $$\Lambda(A)z := f^{-1}_1(Af_1(z) A^H), \ A \in SL_2\mathbb{C}, z \in \mathbb{C}^2.$$ This is indeed a group homomorphism, which is 2:1, meaning that for $\Lambda \in L^{\uparrow}_+$ there are exactly two $A_1, A_2 \in SL_2\mathbb{C}$ which satisfy $F(A_i) = \Lambda, i=1,2.$ More precisely, $A \in F^{-1}(\Lambda) \Leftrightarrow -A \in F^{-1}(\Lambda).$ Now, one can calculate that for a given Lorentz Transformation $\Lambda$ with components $\Lambda_{\mu \nu}$ we have $$\gamma^{\mu}\Lambda^{-1}_{\mu \nu} = \begin{pmatrix}A & 0 \\ 0 & (A^H)^{-1}\end{pmatrix} \gamma_{\nu} \begin{pmatrix}A^{-1} & 0 \\ 0 & A^H \end{pmatrix},$$ where $F(A) = \Lambda$ and $\Lambda^{-1}_{\mu \nu}$ denotes the components of $\Lambda^{-1}$.

Lastly, define the representation $\rho: SL_2 \mathbb{C} \to GL(\mathbb{C}^4)$ by $$\rho(A) = \begin{pmatrix}A & 0 \\ 0 & (A^H)^{-1}\end{pmatrix}.$$

Why do we need ''Spinors''?

It might feel a bit strange, but in order to understand what a spinor is, it is indeed helpful to talk about ''spinors'' without having a real definition. You are propably familiar with the famous Dirac equation $$\gamma^{\mu}\partial_{\mu} \psi(x) + im \psi(x) = 0,$$ where $\psi: \mathbb{R}^{1,3} \to \mathbb{C}^4$ is a smooth function. Now, we demand relativistic invariance of this equation, by which we mean the following: Suppose we are given a Lorentz transformation $\Lambda \in SO(1,3)^+ = L^{\uparrow}_+$, and consider the ''transformed'' coordinates $x'_{\mu}:= \Lambda_{\mu \nu} x_{\nu}$ where, again, $\Lambda_{\nu \mu}$ denotes the compontents of $\Lambda$. Now, as can easily be checked by the chain rule, we have $\partial'_{\mu} =\Lambda^{-1}_{\mu \nu} \partial_{\nu}$. Let $\psi'(x')$ denote the ''transformed'' $\psi$, which is intuitively speaking $\psi(x)$ seen in the new coordinates $x'$. We cannot give a precise definition of $\psi'$, the reason of which will become apparent in a moment. Using these conventions, one writes the transformed Dirac equation $$\gamma^{\mu} \Lambda^{-1}_{\mu \nu} \partial_{\nu} \psi'(x') + i m \psi'(x') = 0$$ $$\Leftrightarrow \rho(A)\gamma^{\mu} \rho(A^{-1}) \partial_{\mu} \psi'(x') + im \psi'(x') = 0.$$ In order for this to be true, we set $$ \psi'(x') = \rho(A) \psi(x),$$ where $A \in SL_2 \mathbb{C}$ satisfies $F(A) = \Lambda$. But this cannot be true, since it does depend on the choice of $A$, meaning that we could equally well choose $\psi'(x') = - \rho(A) \psi(x)$! There is no way to tell which is the correct choice, and on a general manifold, it is not even possible to make a ''consistent'' choice! Now, quantum mechanically this is no problem at all, since $\pm \psi(x)$ does define the same state. However, if one argues that way we would have to introduce ''projective'' spaces and ''projective'' representations, which doesn't really simplify things. So we need a new object, which satisfies the above properties. Clearly, it cannot be just a an element in $\mathbb{C}^4,$ as we have just seen (even though this is the common way to introdce spinors, by means of there transformation property, which is fine and does work, but heavily lacks rigor).

Defining Spinors

How can we remedy the above problem? We need a new space! Since we have to try to consistently choose a sign for $\psi'(x')$ lets start the pedestrian way and instead of $\psi$ we just look on the vectorspace $\mathbb{C}^4$ and try to somehow preserve the information about what matrix $A \in SL_2\mathbb{C}$ which induces the Lorentz transformation $F(A)$. But the easiest way to do this is to simply look at $(A,v) \in (SL_2\mathbb{C}) \times \mathbb{C}^4$. Now, getting a bit less pedestrian, we want $(A,\psi(x))$ to equal $(1, \rho(A)\psi(x))$, since the field $\psi(x)$ on which we are letting the transformation induced by $A$ act has to equal the field $\rho(A)\psi(x)$! Mathematically, this equality is construced by means of an equivalence relation ''$\sim$'', more precisely, we let $$ (A,z) \sim (1, \rho(A)z)$$ which is equivalent to $$(1,z) \sim (A, \rho(A^{-1}) z).$$ Finally, we now look at the space $(SL_2 \mathbb{C} \times \mathbb{C}^4) / \sim$ which is the space of equivalence classes under the above equivalence relation. This is a vector space which is isomorphic to $\mathbb{C}^4$. One then defines a spinor as a smooth function $$\psi: \mathbb{R}^{1,3} \to (SL_2 \mathbb{C} \times \mathbb{C}^4) / \sim.$$

A Remark

One might be quick to point out, that in the above the Lorentz transformations are completly gone. In order to capture them, we need to ''lift'' the covering homomorphism to $$F: \mathbb{R}^{1,3} \times SL_2 \mathbb{C} \to \mathbb{R}^{1,3} \times L^{\uparrow}_+, (x,A) \mapsto (x, F(A))$$ and use so called ''frame bundles''. These give a description of coordinate transformations by means of principal fibre bundles (which right now I do not have the time to dive into). This is indeed needed if one want's to formulate the Dirac equation in our new setting, and one would no longer define a spinor as above but rather as a ''section'' $\psi: \mathbb{R}^{1,3} \to (\mathbb{R}^{1,3} \times SL_2 \mathbb{C}) \times \mathbb{C}^4/ \sim,$ where $\sim$ is an equivalence relation similar to the one defined above. This can all be formulated in the ''trivial case'' but in order to really understand why we need all of this, one needs to know Differential Geometry and Gauge Theory, and what I've written so far is only the tip of a huge iceberg. Thus, Spinors are not an easy thing to understand I'd say!

For further reading

Finally, I would like to mention the book The Geometry of Physics by T. Frankel. If you want to understand the Dirac Equation, Lorentz transformations and all that in this new setting, the book might be a good starting point since it contains differential geoemtry (starting with the basics) and also dives into the awesome stuff which this is needed for, for example, the Dirac equation! It is written in a way which I find very intuitive.

If one knows basic Differential Geometry, I would highly recommend Gauge Theory and Variational Principles by D. Bleecker. However, I found that this is neither an easy read nor written intutively. It is, however, more general than Frankels book.

In case one wants to go even further one might even go all the way and consider the book Spin Geometry by H. Blaine Lawsone and M. Michelsohn, which I consider the toughest of the so far mentioned books, but also the most general.

Answer 2

A spinor is just a vector transforming in a particular representation of the relevant symmetry group ($\mathrm{SO}(3)$ non-relativistically and $\mathrm{SO}(1,3)$ relativistically).

In quantum mechanics, we need to look not only at linear representations but also at projective representations of the symmetry groups, see this Q&A of mine for a lengthy mathematical discussion of this fact.

The finite-dimensional projective representations of the Lorentz group $\mathrm{SO}(1,3)$ are labeled by pairs of half-integers $(s_1,s_2)$. They are true linear representations of the Lorentz group only if $s_1,s_2$ are integer. In general, we call representations with half-integers, i.e. projective representations, "spinorial" and the vectors in the representation space "spinors". For instance, $(1/2,0)$ and $(0,1/2)$ are the left- and right-handed Weyl spinors, and $(1/2,1/2)$ is the Dirac spinor.