3

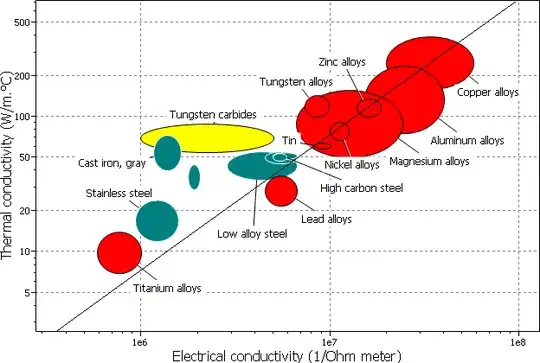
Right off the bat I should say: thermal conductivity and electrical conductivity are definitely correlated in metals.

enter image description here

image source: https://www.doitpoms.ac.uk/tlplib/thermal_electrical/printall.php

But my question: is thermal conductivity correlated with speed of sound in metals? It seemed to me like it should be because-- according to highly rated answers to another question-- the speed of sound is like the "speed of information" about macroscopic deformations. So intuitively I expected faster speed of sound in a metal = faster conduction of heat in that same metal.

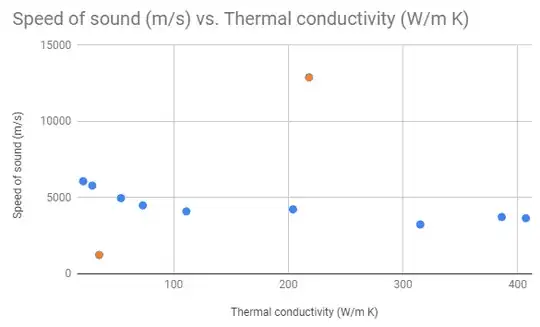
I used data from Engineering Toolbox's pages Speed of Sound in common Solids and Thermal Conductivity of Metals. The speed of sound dataset was the limiting set, so I was only able to get data on both for 11 metals Aluminum, Beryllium, Brass, Copper, Gold, Iron, Lead, Silver, Steel (low carbon steel), Stainless Steel, and Titanium:

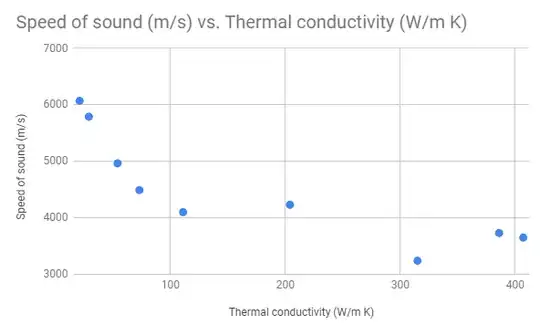
enter image description here

Initially looks like there is no trend. However-- there are two outlier points. Lead and Beryllium are the metals marked in orange instead of blue. The other 9 metals had sound speeds between 3 and 7 thousand m/s. I removed those two from the data:

enter image description here

Here's where I get confused. My assumption was: faster speed of "information" through the metal equals higher thermal conductivity. It looks (to me) like there is a trend and the trend shows the opposite of what I assumed. What am I missing?

pentane
  • 3,072

2 Answers2

2

In metals, there is the Wiedemann-Franz law because in metals heat is carried mostly by electrons.

Alloying reduces the electron mean free path, but it does not affect the speed of sound that much. For example compare copper and brass (a Cu-Zn alloy) or iron and different steel alloys.

In insulators, thermal conductivity is mediated by phonons. Both speed of sound and mean free path are important there. But that was not what the question was about.

2

Generally in solids (be it metals, semiconductors or insulators) the speed of sound has to do with accoustic phonons. The case is more complex for the thermal conductivity.

In metals, heat conduction is mostly due to electrons, rather than phonons. As such, I would say there should not be a high correlation between the speed of sound and the thermal conductivity.

The situation is completely different for insulators where both the speed both of sound and the thermal conductivity have mostly to do with accoustic phonons. In that case the correlation between $\kappa$ and $v_s$ should be high, or much higher than in metals if you prefer.

In semiconductors the situation is in between the one of metals and insulators, with a strong dependence on the doping level. As a general trend, the more heavily they are doped, the more like a metal they behave. And the less they are doped, the more they behave like an insulator.

Note: Brass, steel and stainless steel are alloys.

Edit: Rereading your question, it seems to me like you confused thermal conductivity with the speed of heat propagation. If that's the case, then this is wrong. In a metal, the "speed of heat" (as in real speed, i.e. with units of distance divided by time), is of the order of Fermi speed, so about $10^6 \mathrm{m}/\mathrm{s}$ near room temperature. Again, this is so because it's the speed of heat and charge carriers.

$\kappa$ is related to the rate of heat transfer. The bigger the $\kappa$, the bigger the heat flux through a surface in the solid.

Also, note that the common heat equation $\nabla \cdot (\kappa \nabla T)=C_p\frac{\partial T}{\partial t}$ is a parabolic PDE, meaning it displays an infinite speed of propagation. So it cannot represent perfectly "reality". One has to modify it and transform it to a hyperbolic heat equation in order to account for a finite speed of propagation, as is usually done in relativistic situations.

untreated_paramediensis_karnik
  • 6,250