This model (assuming a square lattice) has been studied in the literature for a while. K Binder and DP Landau Phys Rev B, 21, 1941 (1980) discuss the three possibilities for the ground state: ferromagnetic (F), antiferromagnetic (AF), and superantiferromagnetic (SAF). Basically one considers the likely structures and picks the one with the lowest energy. They also conducted Monte Carlo simulations to determine the phase behaviour at higher temperatures, and never saw any more complicated structures. There's more discussion in J Oitmaa J Phys A, 14, 1159 (1981), and I drew the following diagram based on Fig 1 from that paper.
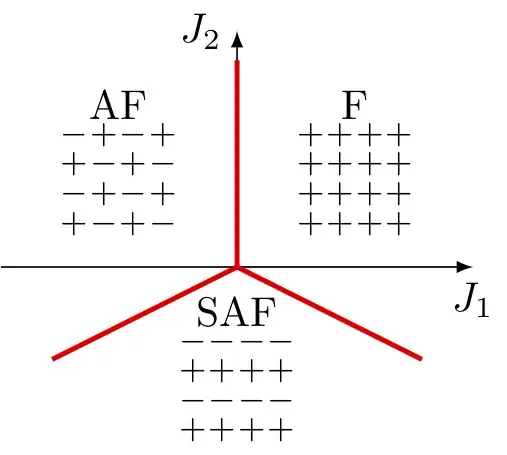
The SAF phase consists of alternating rows of $+$ and $-$ spins in one direction
(which can be horizontal or vertical, giving an additional degeneracy
on top of the usual up-down spin degeneracy).
The relevant energies per spin are
\begin{align*}
E_\text{F}/N &= -2J_1 -2J_2 \\
E_\text{AF}/N &= 2J_1 -2J_2 \\
E_\text{SAF}/N &= 2J_2
\end{align*}
The lines along which SAF becomes energetically equal to either AF or F
correspond to $J_2=-\frac{1}{2}|J_1|$.
So the case in which you are interested, $J_1>0$ and $J_2=-J_1$,
lies well within the SAF region.
There may be discussions of this model in standard texts, but I don't have any of those to hand, sorry, and the papers I cited both require a subscription. There is a connection with the anisotropic next-nearest-neighbour Ising or ANNNI model (which I saw mentioned in a comment on your earlier question), and that model is of interest both experimentally and theoretically.
