Unlike most Planck units named after "Planck" such as Planck length, Planck temperature, etc, the Planck mass seems more closed to daily life. It is about $10^{-5}$g, same order of magnitude of one eyebrow hair or a flea egg.
I am just wondering is there any interesting explanation about the relation between Planck mass and the mass of small lives such as flea.
There is a popular physics book (similar to The Elegant Universe, but different) (EDIT: a comment suggested this is The Black Hole War, and that sounds right, although I can't reference the exact figure) that I remember addressing the significance of the Planck Mass relative to the idea of elementary particles versus black holes. For now, Wikipedia will have to suffice, which I will reference here:
http://en.wikipedia.org/wiki/Planck_mass
The Planck mass can be derived approximately by setting it as the mass whose Compton wavelength and Schwarzschild radius are equal.
So why does this matter? The argument as I remember in the book goes like this:
Both elementary particles and black holes are "singular" objects. An atom, by comparison, is a collection of elementary particles, with structure to boot. A black hole can have almost any given mass. If a particle falls into a black hole, its mass increases by that amount. If you include massless particles, the permitted mass of black holes is almost a continuum. Not so for elementary particles. They have a certain rest mass (if any), and this rest mass comes from the fundamental properties of the universe.
The Planck Mass, the argument goes, is like the boundary between these two regions of elementary particles and black holes. This book had a very good image illustrating this. Unfortunately I can't find it anywhere online, so I will reproduce it here:
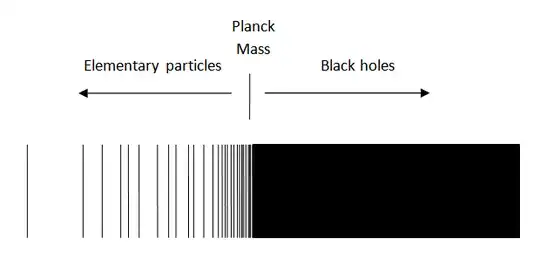
A notable observation is that there are much fewer particles with low rest masses, like the electron. This is consistent with what we know. As particle physics advances, we also produce more high mass particles, like the Higgs. By this line of thinking (which I'm not 100% confident is true), there will be a much higher density of particles at higher masses as they approach the Planck mass. Once you get higher mass than that, you're talking about a valid black hole.
That region, however, is relatively unimportant from a practical perspective because both high mass elementary particles (see again, the Higgs) and low mass black holes are incredibly unstable. Thus, on either side on that divide the particles are particularly short lived. You have to go far right or far left to get something stable.
Allow me to make the obvious argument that the absence of stable particles and black holes at our physical scale is important. Why? Because that means that for the mass ranges from quarks to almost stellar-mass black holes, the universe has no choice but to make complex things, made of many elementary particles, but not collapsed into a black hole. I hope the Anthropic argument is then obvious. We should be thankful that our cells are not commonly intruded by frequently interacting 100s of GeV or TeV particles, as this would not be good for cell chemistry. We can also be thankful that small black holes are not stable... I hope the reason for that is obvious.
The reason the Planck mass is big is the same reason that the Planck length is small--- we are living on a scale which is enormous in Planck units. So everything around us is made from enormous atoms which have tiny, tiny masses, and you need a large number of atoms to make 1 Planck mass, just as you need a large number of Planck lengths to make 1 meter. The inverse relationship is because of the uncertainty principle, short distances are large energies.
The number of atoms you need is roughly the size of a few million cells, so what. It's not very significant, except the cells are about half way from the Planck length to the radius of the universe. The radius of the universe is from the cosmological constant scale, and the Higgs scale is about half-way between the Planck scale and the cosmological scale in log-energy. There's no explanation for this.
No, not really.
If you managed to compress a flea egg so it became a black hole then the conflicting descriptions of General Relativity and Quantum Mechanics could come into play.
But fleas are not able to achieve the extreme density required for this, so the similar magnitude of the two masses is largely irrelevant.
Similarly, the Planck energy unit being the same order of magnitude as the chemical energy in an automobile's gasoline tank is a curiosity but is not significant, except perhaps to suggest that Planck units may not always be fundamental.
Well, this is a question that asks for opinions. In my case I think there exists a tentative relationship between very small live organisms and the Planck mass. From wikipedia
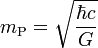= 2.17651(13)×10−8 kg, (or 21.7651 µg)
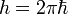The name honors Max Planck because the unit measures the approximate scale at which quantum effects, here in the case of gravity, become important. Quantum effects are typified by the magnitude of Planck's constant,
.
My hand waving argument goes: Live organisms have to exist in a classical environment, where there is evident causality for energy input and surroundings. Therefore the Planck mass must be the lower limit in mass value, in order for a primary seed not to be driven this way and that by quantum mechanical potentials. This would certainly be true if the seeds of life came during the evolution of the Big Bang.
In our earth environment quantum mechanical dimensions are gauged by h, and one would have to check small organisms against that. I see that they are going to atto ( 10^-3 nano) units to measure viruses (viz the comment on the other answer). h is a very small number 6.6*10^-37 ergs sec and evolution could develop smaller sizes than the planck mass without hitting quantum mechanical uncertainties.
Planck mass being so large and "classical", as well as the fact that Planck length and time are extremely small and "quantum mechanical", could point to the possibility that it is not a fundamental unit of mass. It could also point to the possibility that Newton's constant "G" is not a fundamental universal constant but composed of other universal constants like h and c.
