3

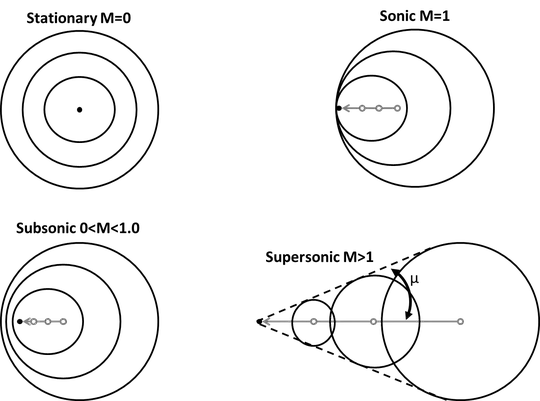
When an object is flying in the air at a mach number ($M$) greater than 1, a shock wave is continuously produced and the mach cone makes a particular angle, $\theta_M$, with the ground (or normal). An observer on the ground will hear a shock wave when their relative angle with the flying object reaches $\theta_M$. But why does the observer not hear continuous shock waves, which are continuously produced by the flying object? If the observer is now inside the mach cone, are not the shock waves propagating spherically symmetric and would not the observer still hear a shock? Would not an observer even directly behind the flying object hear the shock wave using this same logic?

enter image description here

Physically, are the gas molecules just all bunched/compressed exactly at the mach angle for some reason? Based on the derivation of $\theta_M = \arcsin (1/M)$, it appears this is the angle of the flying object relative to when a sound is first heard, but should not an observer continue hearing a sound? In the picture, the black solid lines appear to indicate distinct waves which should be able to be heard by any observers for either subsonic or supersonic motion. I would've thought anyone intersecting the black lines would hear the sound associated to regular waves ($M<1$) or a shock discontinuity ($M>1$). But is that true?

Perhaps I am misunderstanding where the shock front itself exists and this is a crucial premise to the above. Is not a new shock front continuously generated at each time and location? And does not each of these new shock fronts continuously expand spherically? Unless I am mistaken, this is what the pictures depicts and one should hear multiple shocks (which is contrary to experience).

Mathews24
  • 668
  • 4
  • 20

2 Answers2

3

Think about what sound is. Sound is variations in pressure over time.

Forget about shock waves, and think about the following problem. You are sitting in an enclosed, airtight room, with sound-absorbing walls, and with pressure $p_1$. Suddenly and instantaneously, the pressure in the room increases to $p_2$ and stays at that pressure. What would you hear? A continuous noise, or a single 'bang' or 'puff' during the actual pressure increase? The answer is the latter. In fact, it is possible to perform this very experiment.

Now back to supersonic aircraft. Let us simplify the physics by a large amount and assume that there is nothing else but you and a point-particle plane (no ground, buildings, etc.), with you motionless relative to the air and the plane moving through the air at supersonic speed. A shock wave front compresses the air as it passes through. For all practical purposes, this is an instantaneous increase - it takes on the order of a nanosecond for you to experience the pressure rise so it is essentially instantaneous (and this is why they are so loud, it is a very large change in pressure over very short time). But after the shock wave has passed, there is no longer any sudden change in pressure - you only see a gradual drop in pressure as conditions return to normal. Thus you perceive no additional sound.

Taking your question more literally, and thinking about the more realistic case, you do hear a continuous noise, because even after the shock wave passes, you still hear the shock reflections off of the ground, buildings, etc., plus doppler-shifted engine noise. But I suspect that that's not what you are asking.

EDIT: As to the question of why the shock appears like a cone and not a series of spheres. Shock waves have the characteristic that the fluid downstream of the shock (the 'shocked' fluid) has different properties than the fluid upstream ('unshocked' fluid). In particular, the shocked air is actually moving forward with some velocity, and has higher speed of sound. Thus if you have two simple planar shock fronts, the shock front that is behind tends to 'catch up' to the shock in front, forming a single shock. This is the basic reason why there aren't a series of spherical shocks, and instead a series of combined, conical shocks.

Because of this, a bit of mathematics is involved to actually compute the right shape of each shock wave. Further, as a body moves through a fluid supersonically, shocks are generated whenever there is a change in cross-sectional shape. The two most pronounced shocks, often, are a compression shock at the front of the object, and a rarefaction shock at the end. These two shocks interact with each other in nontrivial ways. For example, because the rarefaction shock is happening in an already-shocked air regime with higher speed of sound, the angle is more acute.

Going into more detail would require analyzing the physics at a deeper level. This book is the classic reference text on the subject, it is not too math-heavy and is easy to read.

A Nejati
  • 3,815
2

In the supersonic regime, the shock wave propagates with the shape of a cone. If a supersonic plane flies close to the ground, you'll hear the sonic boom followed by doppler-shifted engine and airframe noise. Because the shock front is so much more energetic than the engine noise being radiated back away from the plane as it moves, the boom is the only thing you will hear if the plane passes overhead at high altitude.

It is common for a supersonic plane to pull more than one shock along with it. You'll get one shock at the tip of the nose and another at the leading edge of the wing and possibly another at the tail surfaces. this will make for a complex boom noise with more than one major component.

niels nielsen
  • 99,024