3

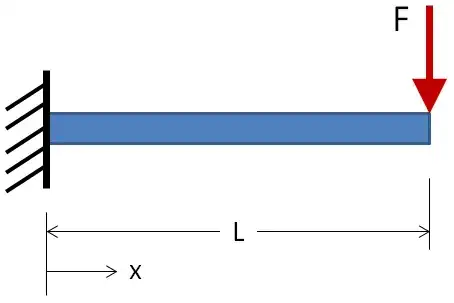
In a beam with a a single vertically applied load and a single vertical reaction force, as well as a reaction moment, for example, this one:

Cantilevered beam with length L and load F applied at unsupported end

We would typically consider the normal stress ($\tau_{xx}(x,y)=\frac{Fxy}{I}$, where $I$ is moment of inertia of the beam vertical cross-section) due to the moment, and the shear stress ($\tau_{xy}(y)=\frac{FQ}{It(x,y)}$, where $Q$ is the first moment of area between $y$ and the neutral axis, and $t(x,y)$ is the thickness of the beam at the point) due to the force, when calculating the effective stress at any point in the range of the beam. We could then, for example, use these stresses to develop an effective stress, $\sigma'$, when determining the factor of safety due to the applied loading.

Why don't we also consider a normal compressive stress $\tau_{yy}$ due to the load and vertical support reaction (ie $\frac{F}{Lt}$)? Is it just too small to matter, or is there no actual stress in that direction?

Ian
  • 147

1 Answers1

3

The normal stress in the transverse direction (y in this case) effectively exist, but the Bernoulli-Euler beam theory does not allow cross sectional deformation (it is assumed to be rigid in its own plane); therefore, although it is possible to calculate the transversal stress generated by Poisson's effect, the results would not be accurate since in reality the cross section is not rigid in its own plane.

Most beam theories are inconsistent in the sense that you can always calculate some stress (using the constitutive law) that is associated to a deformation that was assumed to be zero but it is not actually zero, but small. Then you can always ask yourself if having this value is better than not having it.

If you solve the continuum partial differential equations of equilibrium (almost exclusively a numerical method such as finite elements would be required) you can effetively capture the actual normal stress in the transverse direction.

Lastly, the stress you look for is commonly smaller than the normal stress in the axial direction.

nodarkside
  • 355