The reason I ask this is because many posts imply that electromagnetism is parity invariant as we use the right hand rule twice in many cases, negating its arbitrariness, but here we use it only once.
That last bit is incorrect. If you want a description for the dynamics which depends strictly on vector objects, then you do use the right-hand rule twice.
The core of the field picture is that the only thing that matters is the local value of the field, and not how it was produced. In many situations, there will be multiple different possible origins for how a given local field configuration was produced, and we're free to choose whichever provides the most convenient analysis.
In your case, where you have a particle confined to the $x,y$ plane of the page with a uniform magnetic field going into the page, the cleanest analysis is to provide that magnetic field using a pair of Helmholtz coils above and below the page:
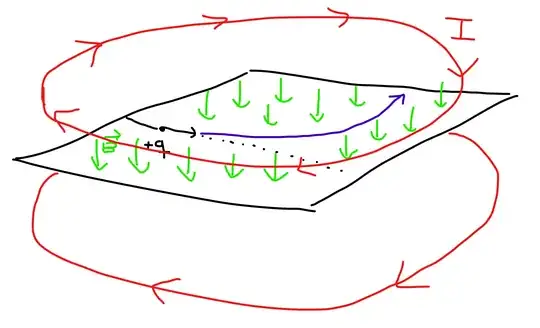
And, once you do that, it's clear that those Helmholtz coils have an intrinsic circularity, and they break the symmetry between 'up' and 'down' for the particle. If you want the particle to go the other way, then change the direction of the current in the coils.
Now, here you'll probably have a perfectly valid observation - that this still doesn't answer the full analysis for the case where the magnetic field is produced by a permanent magnet. Does that require an only-once usage of the right-hand rule? Well, yes and no.
From one perspective, as far as macroscopic electromagnetism goes, a permanent magnet's effect is basically indistinguishable from the magnetization current on its surface. At that level of analysis, a permanent magnet is exactly identical to a coil of wire carrying that current, which brings you back to the case from above.
On the other hand, the physical analysis that allows us to underpin that magnetization current with intuition generally asks that we picture a magnetized material as if it were a bunch of tiny current loops, but that's not really the case. The magnetization in ferromagnetic materials comes from the macroscopic organization of the intrinsic magnetic dipole moments of the electron spins inside the material, and those cannot be thought of as tiny current loops.
Nevertheless, both the magnetization and the electron spin that underpins it are still pseudovector objects, and they're still associated with a sense of rotation on the plane of the page. "Spin" the electrons the other way (i.e. give them an angular momentum in the opposite sense) and you'll change the direction of the magnetic field.
So, actually, no and no: you never require only-once applications of the right-hand rule. It's just that permanent magnets are inherently chiral objects, and when we say "north" or "south" regarding a pole of a magnet, we're really specifying a rotation direction about that axis.
