Giancoli Textbook question:
To make a given sound twice as loud, how should a musician change the intensity of the sound?
The given answer is: "Increase the intensity by a factor of 10."
I don't get it, doesn't increasing it by a factor of 10 contribute +10 decibels and is only correct if the sound is 10 decibels from the start? I'm thinking that it might not be referring to the sound level in dB, but if it does not refer to the sound level, what does it refer to? Thanks for the help.
In psychoacoustic experiments, when asked to turn up the volume twice as high, most people increase the sound level with about 10 dB which is 10 times the intensity.
It is not really a physics thing. It is perception. And natural language.
Edit: The textbook mentions it. In section 12-2 Giancoli writes: "To produce a sound that sounds about twice as loud requires a sound wave that has about 10 times the intensity."
He goes on to say that "four times as loud" is $100$ times the intensity. I would be a bit skeptical about that.
I think you are confusing the relationship between loudness and sound intensity, with the relationship between Sound Intensity Level and sound intensity relative to a reference value, that is expressed by the equation: $$L_I=10 \log_{10}\left(\frac I{I_0}\right) \textrm{dB}$$ What you are talking about in your post is the relationship between loudness, which is the strength of ear's perception of sound, and the physical quantity called the intensity of sound. They are related by the "rule of thumb" that you just described. You can find this information at: http://hyperphysics.phy-astr.gsu.edu/hbase/Sound/loud.html
As others noted, loudness is a psycho-physical sensation perceived by the human auditory perception. It is not the same as sound pressure level, in which doubling the intensity increases the spl by 3db (not 10db), or voltage by 6dB.
See this plot:
Therefore:
Double or twice the loudness [intensity] = factor 2 means about 10 dB more sensed loudness level (psycho acoustic)
Double or twice the voltage [intensity]= factor 2 means 6 dB more measured voltage level (sound pressure level)
Double or twice the power [intensity]= factor 2 means 3 dB more calculated power level (sound intensity level)
EDIT:
Below are the equations for Loudness with respect to intensity ratio (as well as voltage and power)
As you can see, the equation governing loudness is log2 as opposed to the traditional log10. Though it can be represented in log10, the multiplier becomes 33.22 (instead of the traditional 10 or 20 used for power and voltage, respectively)
Giancoli's question and answer are simply nonsense.
If "twice as loud" is interpreted in physical terms, then it means twice the intensity, in units of watts per square meter, and this is then a change of about 3 dB, not 10 dB.
If, on the other hand, "twice as loud" is supposed to be interpreted in psychoacoustic terms, then it's still not really very meaningful, or meaningful only in the sense that if you poll people and ask them to judge what is "twice as loud," their responses, when measured physically, may cluster around some number of dB -- but there is certainly no way to predict this based on having read a freshman physics textbook. This is like asking someone whether something is "twice as sour," or if a puppy is "twice as cute," or if a certain shade of red is "twice as saturated," or if Trump is "twice as evil" as George W. Bush.
Having had the misfortune to have taught from Giancoli, I'm not surprised that there is crap this bad in that book, but wow...this is shockingly bad.
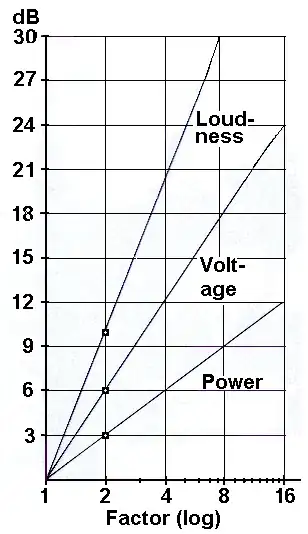
As already mentioned, decibels are on a logarithmic scale: $$L=10\log_{10}\left(\frac{I}{I_0}\right)\ \rm{dB}$$
If we do what the answer says: increase $I$ by a factor of $10$, what happens? $$L'=10\log_{10}\left(\frac{10I}{I_0}\right)\ \rm{dB}=10\log_{10}\left(\frac{I}{I_0}\right)\ \rm{dB}+10\ \rm{dB}$$
So we see that we actually add $10\ \rm{dB}$ to the decibel rating. Whether or not this is "twice as 'loud'" is somewhat subjective, as others have pointed out as well.
If we wanted to actually double the decibels we would have $$2L=10\times2\log_{10}\left(\frac{I}{I_0}\right)\ \rm{dB}=10\log_{10}\left(\frac{I^2/I_0}{I_0}\right)\ \rm{dB}$$
So you would want your intensity to become $$I'=\frac{I^2}{I_0}$$ (i.e., increase by a factor of $\frac{I}{I_0}$)
Which does in fact depend on the initial intensity $I$.
So really either the question could have been written better if this information is not in the book (since it seems like it is looking for a single quantitative correct answer, when there isn't one), or the solution could have gone into what assumptions were being made to arrive at the answer of multiplying the intensity by $10$.
Don't try to establish repeatable settings based on the human hearing response 'trends' documented in psychoacoustics. Psychoacoustics is variable as each person's hearing response is widely variant.
If you play two pure notes 500 Hertz and 600 Hertz at the same amplitude at a comfortable listening level, then adjust the amplitude of one note down, you will reach a point were the lower amplitude sound level note will not be discerned by natural hearing. Yet most likely if you turned off the higher amplitude note, you would then hear the lower amplitude note just fine. Now set the two notes closer in frequency, 500 Hertz and 525 Hertz. Begin adjusting the amplitude of one note downward and you will discover you can no longer hear the lower amplitude note when it is still at a much higher amplitude when compared to the lower amplitude note more widely separated in frequency. This phenomena is often distorted in individuals with hearing loss or other auditory differences in their hearing. If you adjust the starting amplitude up or down when measuring amplitude differential using the loss of perception in the one note as the metric you will find the amplitude differential between the two notes will vary dramatically.
Psychoacoustics is a good tool to understand there why there is a differential in hearing response but to compare sound levels you still need to rely on physically measured properties and not the widely variant individual perception when quantifying properties.
