3

I have used an ab initio electronic structure code to calculate the harmonic Raman spectrum of a (molecular) crystal. However, no use of symmetry has been made, and it might well be that some of the vibrational modes that I obtained are actually Raman-inactive. As a matter of fact, when I consider a single cell, two of the vibrational modes I obtain have a high Raman intensity, but when I double the size of the cell, these two modes seem to fuse into a single mode of much lower intensity (not zero, but...). My question(s) would thus be the following.

  1. Looking at a specific calculated vibrational mode, how can I say whether it is Raman-active or not ? I think I first have to determine the symmetry of my mode, and see if it has the same symmetry as one component of the polarizability tensor, but I'm not sure how to do this, as I am a bit confused with point/space groups. Maybe there is also another way.
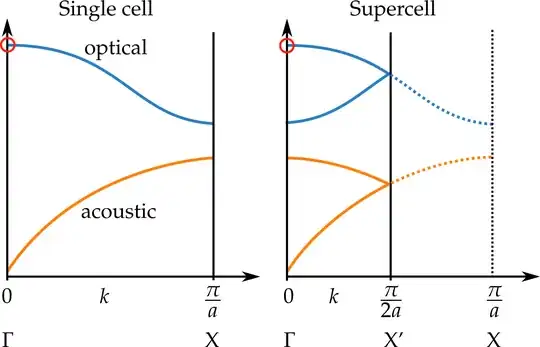
  2. Looking at a specific calculated vibrational mode in a single cell, can I determine what this mode would look like for the double-sized cell ?

Some more information:

  • My system contains 80 atoms (4 molecules) per unit cell, and its space group is P2$_1$/a.
  • The two modes I'm talking about are methyl group rotations.

  • The information about the vibrational modes is stored as an xyz file, containing, in order, the atom type, the position, and the eigenvector (basically, a vector "sits" on every atom). The file would look like this:

    80 stable frequency at 155.045 1/cm Raman int. is 1.6100E+02 Ang^4/amu; red. mass is 1.807 a.m.u.; force const. is 0.026 mDyne/Ang. C 8.3725 5.4769 9.6155 -0.0071 0.0657 -0.0516 H 8.2818 6.5453 9.3705 0.2118 0.0540 -0.1846 H 7.6925 5.2982 10.4580 -0.1575 0.2755 -0.1301 H 9.4066 5.2741 9.9201 -0.0804 -0.0702 0.1096 ... C 6.3734 10.0506 7.9586 0.0071 0.0657 0.0516 H 5.3393 9.8479 7.6541 0.0804 -0.0703 -0.1096 H 7.0533 9.8719 7.1161 0.1575 0.2755 0.1301 H 6.4642 11.1191 8.2036 -0.2118 0.0540 0.1846 ...

Thank you in advance!

Leinahtan
  • 53

1 Answers1

2

In principle you should determine the irreducible representation of the mode, i.e. how its eigenvector transforms under the symmetry operation of the space group, and look up whether the irreducible representation is Raman active. The Raman tensors for all space groups can be found at the Bilbao crystallographic server. If your irreducible representation is listed your mode is Raman active. Most ab initio codes support a symmetry analysis of the Raman and IR modes, i.e. phonon modes at the $\Gamma$ point

For your space group P2$_1$/a with point group $C_{2h}$ there are two gerade, Raman active irreducible representations, $A_g$ and $B_g$ and two ungerade Raman inactive irreducible representations, $A_u$ and $B_u$.

Your second question is based on the misconception that the the super cell is a physically different system than the single cell, which is not true. The translational symmetry of crystals is baked into solid state theory and both descriptions, super and single cell must yield the same results. Now you might ask: "Why do I get twice as many modes with my super cell?".

Raman and IR modes are nothing more than phonon modes at the $\Gamma$ point, i.e. $k=0$. Solid state theory tells us that only phonon modes with almost (dipole) or exactly zero (Raman) contribute to dipole interaction and Raman scattering Phonon modes are described through a phonon dispersion with respect to the k vector. The k vector basically tells you how the phase of a certain mode changes over several unit cells.

When you double the cell in real space you cut k space in half. All phonon branches that extend into the cut region are folded back as indicated by the figure below.

enter image description here

However the single cell description is still valid. Only the modes that originally were IR or Raman active (indicated by the red circle in the image) are IR or Raman active in the supercell calculation. The supercell has a new symmetry operation, namely a translation by a half lattice vector. The new modes at $\Gamma$ transform with -1 character under this transformation and are therefore light inactive.

You can also predict the shape of the new modes. It is simply $$\begin{align} l_{ij}' = l^X_{ij} \exp{\left(-i \mathbf{k}_X \mathbf{R}_i \right)} \end{align}$$ with $l_{ij}$ the original eigenvector component, however at the X point, of nucleus $i$ and coordinate $j=x,y,z$, the nuclear positions $\mathbf{R}_i$ and k vector at the X point, e.g. $\mathbf{k}_X = \frac{\pi}{a} \mathbf{e}_x$

Community
  • 1
Jannick
  • 1,283
  • 8
  • 15