5

In a Griffiths problem (3.4) I'm asked to find the average electric field over the surface of a sphere due to point charges inside/outside the surface. The calculation is done in his solutions starting with some point charge a distance $z$ away from the origin, and then integrating the electric field over the surface of the sphere and dividing by the total area:

$\mathbf{E}_{ave} = \frac{1}{A} \int_A \mathbf{E} dA$.

This calculation is all well and good to me, but I'm asked by my job to make a solution video to this problem, and the solution they provide me first finds the average potential over the surface, then takes the gradient to find the average electric field:

$V_{ave} = \frac{q}{4\pi\epsilon_0z}, \implies \mathbf{E}_{ave} = -\partial_z V_{ave} \hat{\mathbf{z}} = \frac{q}{4\pi\epsilon_0 z^2} \hat{\mathbf{z}}.$

This doesn't make much sense to me. In the end you get the average potential as a function of $z$, but it's not the potential at $z$, it's just the average over the sphere given some fixed $z$. By taking the gradient you get the right answer, but I feel that this is a coincidence, since I don't think a derivative with respect to $z$ means what it should here. Is this correct?

Edit: Griffiths Introduction to Electrodynamics, 4e.

Rourke Sekelsky
  • 115

1 Answers1

4

enter image description here

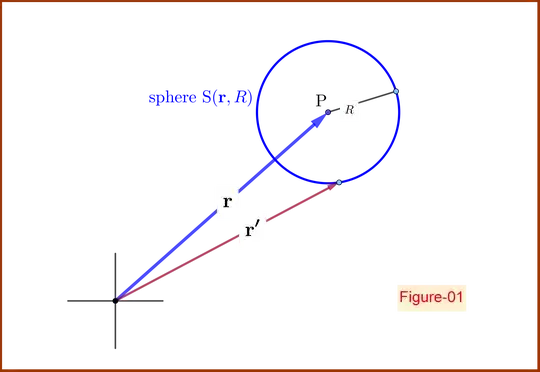
In electrostatics we have \begin{equation} \mathbf{E}\left(\mathbf{r}\right)=\boldsymbol{-\nabla_{\mathbf{r}}} V\left(\mathbf{r}\right) \tag{01}\label{eq01} \end{equation} In a region free of charges the electrostatic potential $\;V\left(\mathbf{r}\right)\;$ at a point $\;\mathrm P\;$ with position vector $\;\mathbf{r}\;$ is equal to the average potential on a spherical surface $\,\mathrm S(\mathbf{r},R)\,$with center at $\;\mathrm P\;$ and radius $\;R$, see Figure-01 above \begin{equation} V\left(\mathbf{r}\right)=\dfrac{1}{4\pi R^2}\!\!\oint\limits_{\mathrm S(\mathbf{r},R)}\!V\left(\mathbf{r'}\right)\mathrm{dS}=V_{\bf ave}^{\mathrm S} \tag{02}\label{eq02} \end{equation} Note that this value is independent of the radius $\;R\;$ of the sphere as long as it does not contain charges. Inserting expression \eqref{eq02} in equation \eqref{eq01} we have \begin{equation} \mathbf{E}\left(\mathbf{r}\right)=\boldsymbol{-\nabla_{\mathbf{r}}}\left[\dfrac{1}{4\pi R^2}\!\!\oint\limits_{\mathrm S(\mathbf{r},R)}\!\!V\left(\mathbf{r'}\right)\mathrm{dS}\right] \tag{03}\label{eq03} \end{equation} Now we must examine if in the rhs of equation \eqref{eq03} it's permissible to insert into the integral the gradient $\;\boldsymbol{\nabla_{\mathbf{r}}}\;$ with respect to $\;\mathbf{r}\;$ as gradient $\;\boldsymbol{\nabla_{\mathbf{r'}}}\;$ with respect to $\;\mathbf{r'}$. In this case \begin{equation} \mathbf{E}\left(\mathbf{r}\right)=\dfrac{1}{4\pi R^2}\!\!\oint\limits_{\mathrm S(\mathbf{r},R)}\!\!\bigl[\boldsymbol{-\nabla_{\mathbf{r'}}}V\left(\mathbf{r'}\right)\bigr]\mathrm{dS}=\dfrac{1}{4\pi R^2}\!\!\oint\limits_{\mathrm S(\mathbf{r},R)}\!\!\mathbf{E}\left(\mathbf{r'}\right)\mathrm{dS}=\mathbf{E}_{\bf ave}^{\mathrm S} \tag{04}\label{eq04} \end{equation}

That from \eqref{eq03} we could have \eqref{eq04} is proved below.

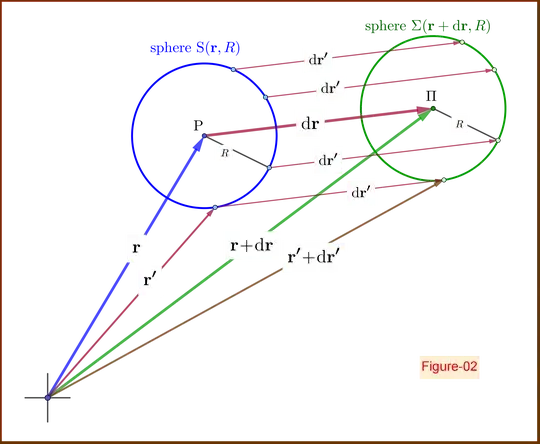
Proof (see Figure-02 in the bottom)

\begin{equation} V\left(\mathbf{r}+\mathrm d\mathbf{r} \right)=\dfrac{1}{4\pi R^2}\!\!\oint\limits_{\mathrm \Sigma(\mathbf{r}+\mathrm d\mathbf{r},R)}\!\!\!V\left(\mathbf{r'}+\mathrm d\mathbf{r}\right)\mathrm{d\Sigma}\stackrel{\mathrm d\mathbf{r}\equiv\mathrm d\mathbf{r'}}{=\!=\!=\!=}\dfrac{1}{4\pi R^2}\!\!\oint\limits_{\mathrm \Sigma(\mathbf{r}+\mathrm d\mathbf{r},R)}\!\!\!V\left(\mathbf{r'}+\mathrm d\mathbf{r'}\right)\mathrm{d\Sigma} \tag{05}\label{eq05} \end{equation}

\begin{align} V\left(\mathbf{r}+\mathrm d\mathbf{r} \right)-V\left(\mathbf{r}\right)& =\dfrac{1}{4\pi R^2}\!\!\oint\limits_{\mathrm S(\mathbf{r},R)}\!\bigl[V\left(\mathbf{r'}+\mathrm d\mathbf{r'}\right)-V\left(\mathbf{r'}\right)\bigr]\mathrm{dS} \nonumber\\ &= \dfrac{1}{4\pi R^2}\!\!\oint\limits_{\mathrm S(\mathbf{r},R)}\!\biggl[\dfrac{V\left(\mathbf{r'}+\mathrm d\mathbf{r'} \right)-V\left(\mathbf{r'}\right)}{\mathrm d\mathbf{r'}}\biggr]\boldsymbol{\cdot}\mathrm d\mathbf{r'}\mathrm{dS} \nonumber\\ &\stackrel{\mathrm d\mathbf{r'}\equiv\mathrm d\mathbf{r}}{=\!=\!=\!=}\left( \dfrac{1}{4\pi R^2}\!\!\oint\limits_{\mathrm S(\mathbf{r},R)}\!\biggl[\dfrac{V\left(\mathbf{r'}+\mathrm d\mathbf{r'} \right)-V\left(\mathbf{r'}\right)}{\mathrm d\mathbf{r'}}\biggr]\mathrm{dS}\right)\boldsymbol{\cdot}\mathrm d\mathbf{r} \tag{06}\label{eq06} \end{align}

\begin{equation} \dfrac{V\left(\mathbf{r}+\mathrm d\mathbf{r} \right)-V\left(\mathbf{r}\right)}{\mathrm d\mathbf{r}} = \dfrac{1}{4\pi R^2}\!\!\oint\limits_{\mathrm S(\mathbf{r},R)}\!\biggl[\dfrac{V\left(\mathbf{r'}+\mathrm d\mathbf{r'} \right)-V\left(\mathbf{r'}\right)}{\mathrm d\mathbf{r'}}\biggr]\mathrm{dS} \tag{07}\label{eq07} \end{equation}

\begin{equation} \lim_{\mathrm d\mathbf{r}\rightarrow\boldsymbol{0} }\dfrac{V\left(\mathbf{r}+\mathrm d\mathbf{r} \right)-V\left(\mathbf{r}\right)}{\mathrm d\mathbf{r}} = \dfrac{1}{4\pi R^2}\!\!\oint\limits_{\mathrm S(\mathbf{r},R)}\!\biggl[\lim_{\mathrm d\mathbf{r'}\rightarrow\boldsymbol{0}}\dfrac{V\left(\mathbf{r'}+\mathrm d\mathbf{r'} \right)-V\left(\mathbf{r'}\right)}{\mathrm d\mathbf{r'}}\biggr]\mathrm{dS} \tag{08}\label{eq08} \end{equation}

\begin{equation} \dfrac{\mathrm d V\left(\mathbf{r}\right)}{\mathrm d\mathbf{r}} = \dfrac{1}{4\pi R^2}\!\!\oint\limits_{\mathrm S(\mathbf{r},R)}\!\!\!\dfrac{\mathrm d V\left(\mathbf{r'}\right)}{\mathrm d\mathbf{r'}}\mathrm{dS} \tag{09}\label{eq09} \end{equation}

\begin{equation} \boldsymbol{\nabla_{\mathbf{r}}} V\left(\mathbf{r}\right) = \dfrac{1}{4\pi R^2}\!\!\oint\limits_{\mathrm S(\mathbf{r},R)}\!\!\boldsymbol{\nabla_{\mathbf{r'}}}V\left(\mathbf{r'}\right)\mathrm{dS} \tag{10}\label{eq10} \end{equation}

enter image description here

VoulKons
  • 16,825
  • 2
  • 45
  • 73