(I'm repeating myself a lot here, but it's because I want to make my confusion clear.)
If 2 billiard balls are the same exact mass, and one hits another stationary one head on, I have heard that the hitting ball will often stop entirely while the one which got hit will go off at the original velocity of the first one (ignoring friction and heat and other potential loss of energy).
I understand that this agrees with conservation of momentum. However, now that I am thinking about it, I am a little confused as to how it is possible.
Consider:
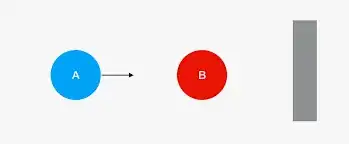
Let's say we have 2 balls, Ball 1 and Ball 2. The balls have equal mass. $$M_{1} = M_2$$
Ball 1 is the hitting ball, with an original velocity of $V_1$, and Ball 2 is getting hit, originally stationary.
Once Ball 1 hits Ball 2, it immediately starts accelerating it at the same rate that it decelerates. In other words, Ball 1 exerts the same force on Ball 2 that Ball 2 exerts on Ball 1. In this way, momentum is conserved, so that for any amount of momentum that Ball 2 gains, Ball 1 loses.
$$F_{1 \to 2} = F_{2 \to 1}$$
That's just Newton's third law.
Since they have the same mass, Ball 1 will decelerate at the same rate Ball 2 accelerates.
However, after a certain amount of time, both balls will have the same amount of momentum in the same direction. That is, Ball 1 will have been decelerated to ${V_{i}/2}$ and ball 2 will have been accelerated to ${V_{i}/2}$.
Ball 1 and Ball 2 at this point of equal momentum must have the same velocity, since they have the same mass.
Now, the only way for Ball 1 to exert a force on Ball 2 is for them to be in contact. However, the instant after they gain the same velocity, the 2 balls would no longer be in contact, as Ball 2 would now be moving away from Ball 1, or at least at the same rate as Ball 1.
That being said, it seems impossible that Ball 2 would ever become faster than Ball 1, since Ball 2 would only be able to be accelerated up to the point where it is going at the same velocity as Ball 1.
And it seems even more impossible for Ball 1 to stop completely and Ball 2 to go off at the original velocity of Ball 1.
What am I missing?
EDIT:
After reading some scrupulous comments, (not in a bad way though, I love it when there are new variables introduced and things pointed out, and all the "what if" questions allways make for awesome discussion, thanks for the comments!) I've realized its better to imagine the billiard balls as floating through space than on a pool table, to get rid of the possibility that spin will affect the collision.
Or we could just imagine a frictionless pool table.
But better to imagine them floating through space, because everyone loves space