I will give an answer to my own question by showing the inverse case (as claimed by user my2cts): Given that there is a 4-vector $j$ that satisfies $\partial_{\mu} j^{\mu}$, one can show that the integral of the component of $j$, which is perpendicular to a spacelike 3-dimensional hypersurface, performed over this surface, will always be the same.
The Proof only holds if all compononents of $j$ become 0 when we spatially go to infinity.
Use 2 sets of base vectors ($\{ e_0, e_1, e_2, e_3 \}$ and $\{ \tilde{e_0}, \tilde{e_1}, \tilde{e_2}, \tilde{e_3} \}$, that are connected by an active lorentz transformation $\Lambda^{-1}$ with $\Lambda^{-1}(e_{\mu}) = \tilde{e_{\mu}}$.
Both sets of base vectors give rise to 2 spatial 3 dimensional hypersurfaces, $S_1$ and $S_2$, which will be spanned by $\{e_1, e_2, e_3 \}$ and $\{, \tilde{e_1}, \tilde{e_2}, \tilde{e_3} \}$.
Imagine hypersurface $S_1$ to be anchored at the point located at (using the first base) the coordinates (0, 0, 0, 0), while the 2nd one, $S_2$, is supposed to be located at (also using the first base)
(T, 0, 0, 0).
Now look at a 4-dimensional Volume, which on its "top" and its "bottom" side is bordered by $S_1$ and $S_2$, while its Sides" lie outside the region where $j\neq0$.
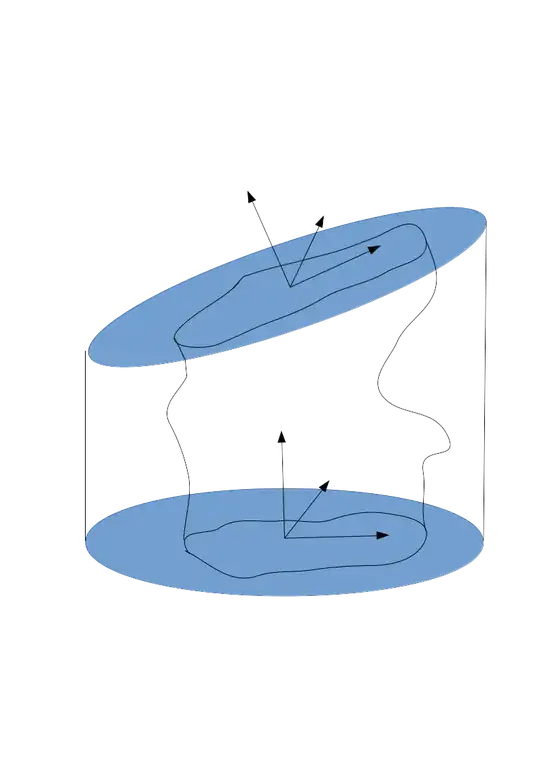The picture shows how it's meant to be, the black linings show the area where $j$ deviates from 0.
Now (indexed quantities like $j^{\mu}$ refer to components of the base-indepedent objects in the first base. $\omega$ is supposed to be the 4-dimensional volume form.
\begin{align}
\int_V 0 \omega = \int_{V} 0 dx^0 \wedge dx^1 \wedge dx^2 \wedge dx^3 = 0 = \int_{V} \partial_{\mu} j^{\mu} dx^0 \wedge dx^1 \wedge dx^2 \wedge dx^3
\end{align}
Because of the (general) stokes-theorem for integration of differential forms, this is the same as
\begin{align}
0=\int_{\partial V} j^0 dx^1 \wedge dx^2 \wedge dx^3 + j^1 dx^0 \wedge dx^2 \wedge dx^3 + j^2 dx^0 \wedge dx^1 \wedge dx^3 + j^3 dx^0 \wedge dx^1 \wedge dx^2
\end{align}
We note at this point that $f = \omega(j, \cdot, \cdot, \cdot)= j^0 dx^1 \wedge dx^2 \wedge dx^3 + j^1 dx^0 \wedge dx^2 \wedge dx^3 + j^2 dx^0 \wedge dx^1 \wedge dx^3 + j^3 dx^0 \wedge dx^1 \wedge dx^2$
gives a 3-form, whiches exterior derivative $d f = \partial_{\mu} j^{\mu} dx^0 \wedge dx^1 \wedge dx^2 \wedge dx^3$ is zero.
Because the regions at the sides don't contribute to the integral anyways, the integration must only be performed over the hyper surfaces $S_1$ and $S_2$. So we know:
\begin{align}
\int_{S_1} f = \int_{S_2} f
\end{align}
Let us now calculate those integrals:
\begin{align}
\int_{S_1} f = \int dx dy dz f(e_1, e_2, e_3) = \int dx dy dz j^0 = c Q_1
\end{align}
It is important to note here that the components of f, with respect to the base ($\tilde{dx}^1 \wedge \tilde[{dx}^2 \wedge \tilde{dx}^3$) transform like the components of a vector (which is intuitive, since the $j^{\mu}$ ARE the components of a vector!).
So we have
\begin{align}
f = \omega(j, \dot, \dot, \dot)= \tilde{j}^0\tilde{ dx}^1 \wedge \tilde{dx}^2 \wedge \tilde{dx}^3 + \tilde{j}^1 \tilde{dx}^0 \wedge \tilde{dx}^2 \wedge \tilde{dx}^3 + \tilde{j}^2 \tilde{dx}^0 \wedge \tilde{dx}^1 \wedge tilde{dx}^3 +\tilde{ j}^3 \tilde{dx}^0 \wedge \tilde{dx}^1 \wedge \tilde{dx}^2
\end{align}
Then the second integral computes to:
\begin{align}
\int_{S_2} f = \int dx dy dz f(\tilde{e_1},\tilde{ e_2}, \tilde{e_3}) = \int dx dy dz \tilde{j}^0 = c Q_2
\end{align}
The total charge contained in the two hyper-surfaces is the same! Since charge conservation holds, this is not only true for this special choice of hyper-surfaces, but as well for $S_2$ to be anchored at any point.
To give an answer to my own question, the invariance of charge holds for any spacelike hypersurface that covers the region with $j \neq 0$. This hypersurface can (in the right frame of reference) be regarded as a spatial volume.
